Let ABC be a triangle with AB=AC. If D is the midpoint of BC,E is the foot of the perpendicular drawn from D to AC,andF is the midpoint of DE, then prove that AF is perpendicular to BE.Solution in Tamil
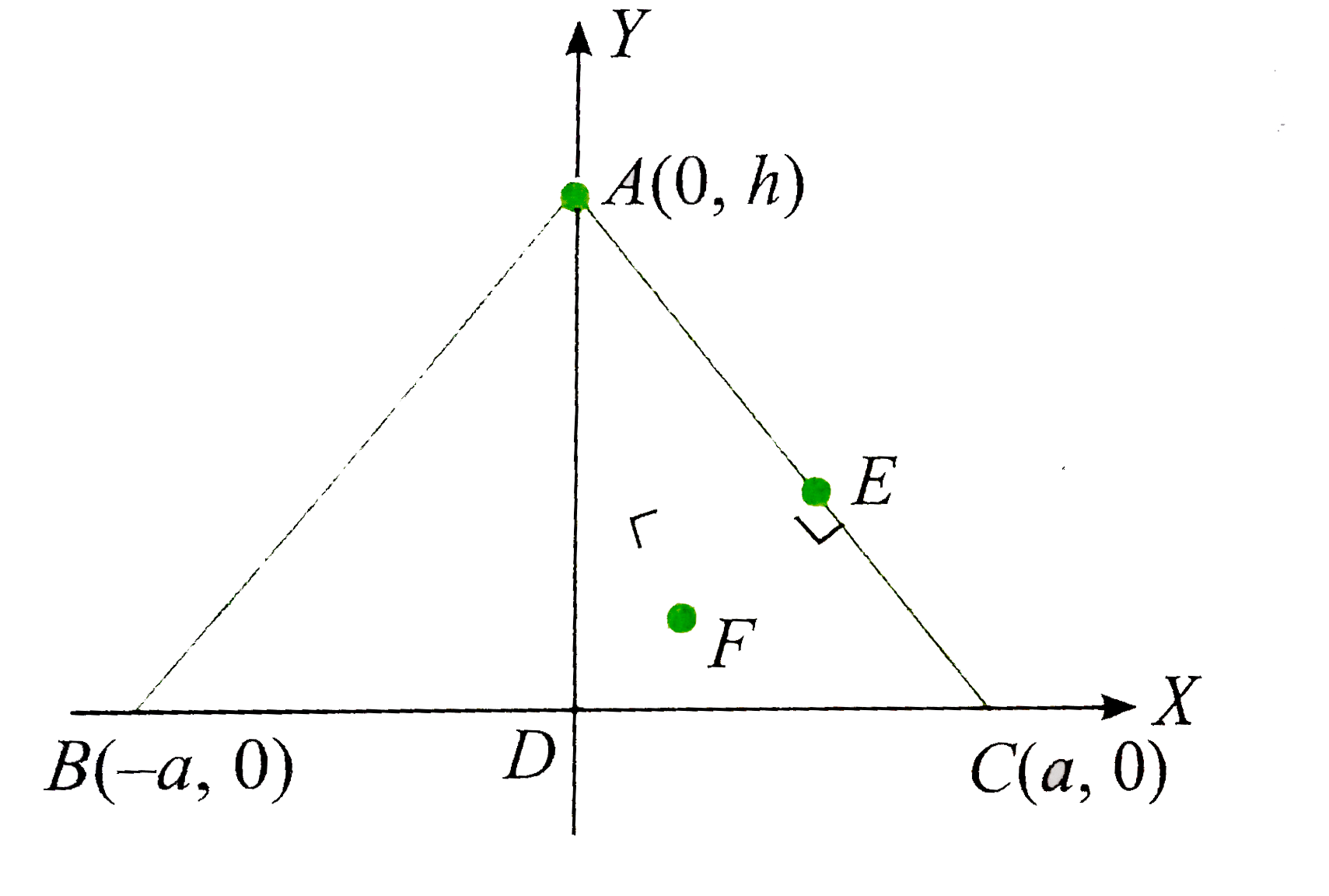
Let BC be taken as the x-axis with the origin at D. Let A be taken on y-axis. Let BC=2a. Now AB=AC, then the coordinates of B and C are (-a,0) and (a,0), respectively. Let DA =h. Then the coordiantes of A are (0,h).
Hene, the equation of AC is ltbgt xa+yh=1 (1)
and the equation of DE perpendicular to AC and passing through the origin is
xh−ya=0
or x=hya (2)
Solving (1) and (2), we get the coordinates of E as follows:
hya2+yh=1
or h2y+a2y=a2h
or y=a2ha2+h2
∴x=aha2+h2
∴E≡(ah2a2+h2,a2ha2+h2)
Since F is the midpoint of DE, its coordinates are
(ah22(a2+h2),a2h2(a2+h2))
The slope of AF is
m1=h−a2h2(a2+h2)0−ah22(a2+h2)
2h(a2+h2)−a2h−ah2=a2+2h2ah (1)
and the slope of BE is
m2=a2ha2+h2−0ah2a2+h2+a
=a2hah2+a3+ah2=aha2+2h2 (2)
From (1) and (2), we have
m1m2=−1
or AF⊥BE
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.123videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.24videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year9videos
THEORY OF EQUATIONS
Similar Questions
Find the equation of the right bisector of the line segment joining the points (3,4) and (−1,2).
12:05View SolutionFind the points on the line x + y = 1 that lie at a distance 3 units from the line 5x+12y = 3.
02:10View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
03:25View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
02:07View SolutionLet ABC be a triangle with AB=AC. If D is the midpoint of BC,E is the foot of the perpendicular drawn from D to AC,andF is the midpoint of DE, then prove that AF is perpendicular to BE.
06:27View SolutionIf in two triangles ABC and DEF , ABDE=BCFE=CAFD , then FDECAB (b) FDEABC (c) CBAFDE (d) BCAFDE
11:20View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of ABC. Then DEF is congruent to triangle. ABC (b) AEF (c) BFD, CDE (d) AFE, BFD, CDE
Given : D, E, F are the mid-point of the sides BC, CA and AB .
04:05View SolutionIn Figure, AB⊥BEandFE⊥BE.If BC=DEandAB=EF, then ABD is congruent to:
(a)EFC
(b) ECF
(c) CEF
(d) FEC
 02:06View Solution
02:06View SolutionD,E,andF are the middle points of the sides of the triangle ABC , then (a) centroid of the triangle DEF is the same as that of ABC (b) orthocenter of the tirangleDEF is the circumcentre of ABC
02:41View SolutionLet ABC be a triangle with AB=AC. If D is the midpoint of BC,E is the foot of the perpendicular drawn from D to AC,andF is the midpoint of DE, then prove that AF is perpendicular to BE.
03:33View SolutionBD and CE are bisectors of ∠B and ∠C of an isosceles ABC with AB=AC. Prove that BD=CE.
04:05View SolutionIf in two triangles ABC and DEF , ABDE=BCFE=CAFD , then FDECAB (b) FDEABC (c) CBAFDE (d) BCAFDE
05:07View SolutionIn Figure, it is given that AE=AD and BD=CE. Prove that AEB ≅ADC
02:57View SolutionIn Figure, AC=AE, AB=AD and ∠BAD=∠EAC. Prove that BC=DE
03:01View SolutionIn Figure, AC=BC, ∠DCA=∠ECB and ∠DBC=EAC. Prove that triangle DBC and EAC are congruent, and hence DC=EC and BD=AE
02:50View SolutionIn Figure, AD=AE and D and E are points on BC such that BD=EC. Prove that AB=AC
04:58View Solution

