Let ABC be a given isosceles triangle with AB=AC . Sides ABandAC are extended up to EandF, respectively, such that BExCF=AB2. Prove that the line EF always passes through a fixed point.Solution in Tamil
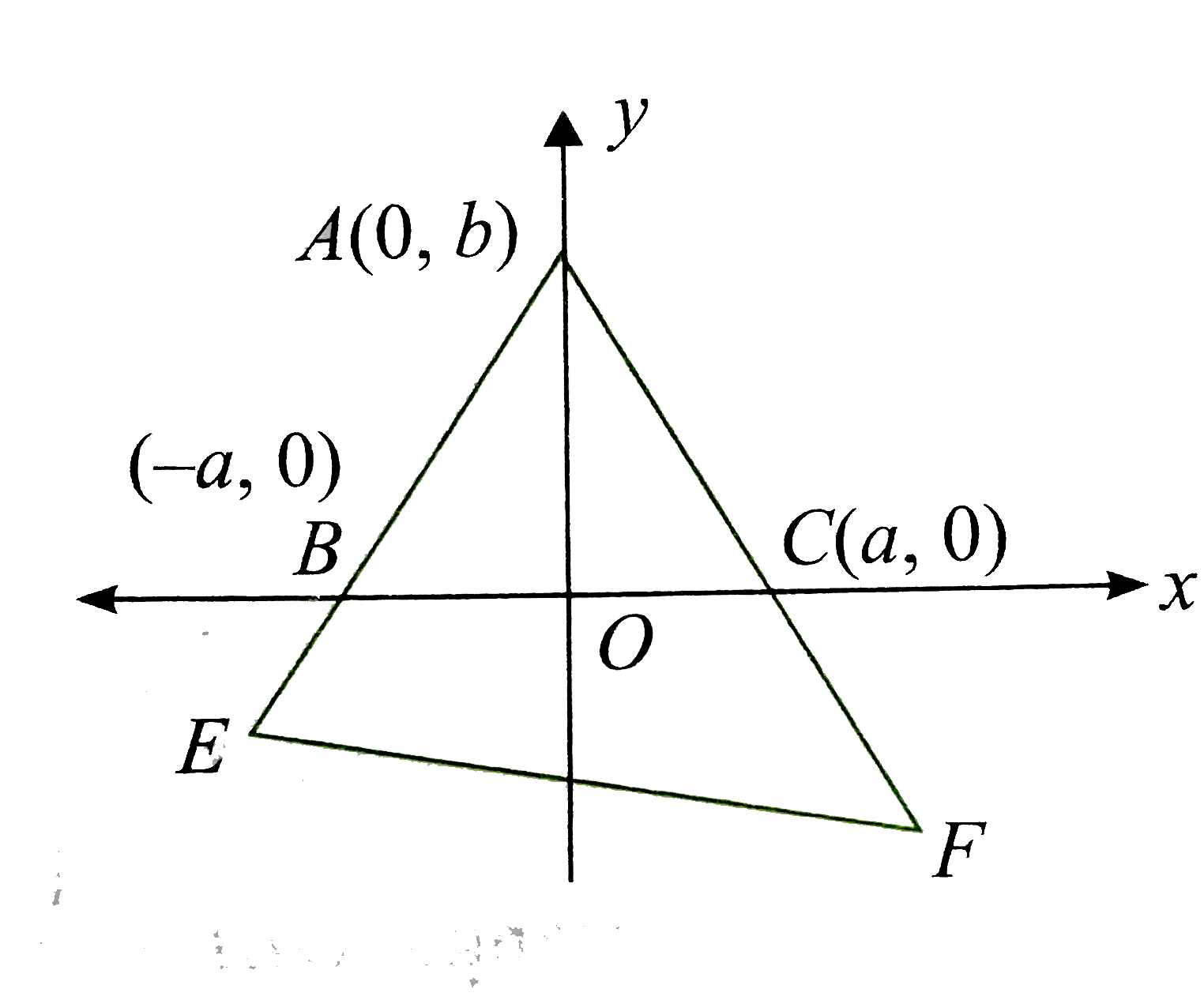
Let ABC be the triangle having vertices (-a,0), (0,b), and (a,0), Now,
BE×CF=AB2
or BEAB=ABCF=λ(Let)
or BEAB=ACCF=λ
Hence, the coordinates of E and F are (−a(λ+1),−λb) and (a(1+1/λ),−b/λ).The equation of line EF is
y+λb=−λb+bλ−a(λ+1)−a(λ+1)λ=[x+a(λ+1)]
or y+λb=bλ(1−λ2)−a(λ+1)λ[1+λ]=[x+a(λ+1)]
or y+λb=b(λ−1)a(λ+1)[x+a(λ+1)]
or a(λ+1)y+abλ(λ+1)=b(λ−1)x+ab(λ2−1)
or (bx+ay+ab)−λ(bx−ay−ab)=0
which is the equation of a family of lines passing through the point of intersection of the lines bx+ay+ab=0 and bx-ay-ab=0, the point of intersection being (0,-6). Hence, the line EF passes through a fixed point.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.123videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.24videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year9videos
THEORY OF EQUATIONS
Similar Questions
Find the equation of the right bisector of the line segment joining the points (3,4) and (−1,2).
12:33View SolutionFind the points on the line x + y = 1 that lie at a distance 3 units from the line 5x+12y = 3.
09:03View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
04:52View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
02:38View SolutionLet ABC be a given isosceles triangle with AB=AC . Sides ABandAC are extended up to EandF, respectively, such that BExCF=AB2. Prove that the line EF always passes through a fixed point.
07:47View SolutionIf D,E,andF are three points on the sides BC,AC,andAB of a triangle ABC such that AD,BE,andCF are concurrent, then show that BD⋅CE⋅AF=DC⋅EA⋅FB .
11:57View SolutionLet D,EandF be the middle points of the sides BC,CAandAB, respectively of a triangle ABC. Then prove that →AD+→BE+→CF=→0 .
04:24View SolutionIn triangle ABC ,points D,EandF are taken on the sides BC,CAandAB, respectively, such that BDDC=CEEA=AFFB=n. Prove that △DEF=n2−n+1(n+1)2△(ABC).
03:58View SolutionFrom a point O inside a triangle ABC, perpendiculars OD,OEandOf are drawn to rthe sides BC,CAandAB, respecrtively. Prove that the perpendiculars from A,B,andC to the sides EF,FDandDE are concurrent.
03:15View SolutionLet ABC be a given isosceles triangle with AB=AC . Sides ABandAC are extended up to EandF, respectively, such that BExCF=AB2. Prove that the line EF always passes through a fixed point.
03:48View SolutionLet D,EandF be the middle points of the sides BC,CAandAB, respectively of a triangle ABC. Then prove that →AD+→BE+→CF=→0 .
07:14View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at EandF . Prove that EBFD is a parallelogram.
03:24View SolutionIn an isosceles triangle ABC with AB=AC, a circle passing through B and C intersects the sides ABandAC atDandE respectively. Prove that DE∣∣BC.
06:41View SolutionABC is an isosceles triangle in which AB=AC. If DandE are the mid-points of ABandAC respectively, prove that the points B,C,DandE are concylic.
06:50View SolutionIf D,EandF are three points on the sides BC,CAandAB, respectively, of a triangle ABC such that the BDCD,CEAE,AFBF=−1
08:03View Solution

