ABCD is a square A≡(1,2),B≡(3,−4). If line CD passes through (3,8), then the midpoint of CD is Solution in Tamil
(2,6)
(6,2)
(2,5)
(28/5,1/5)
The correct Answer is:D
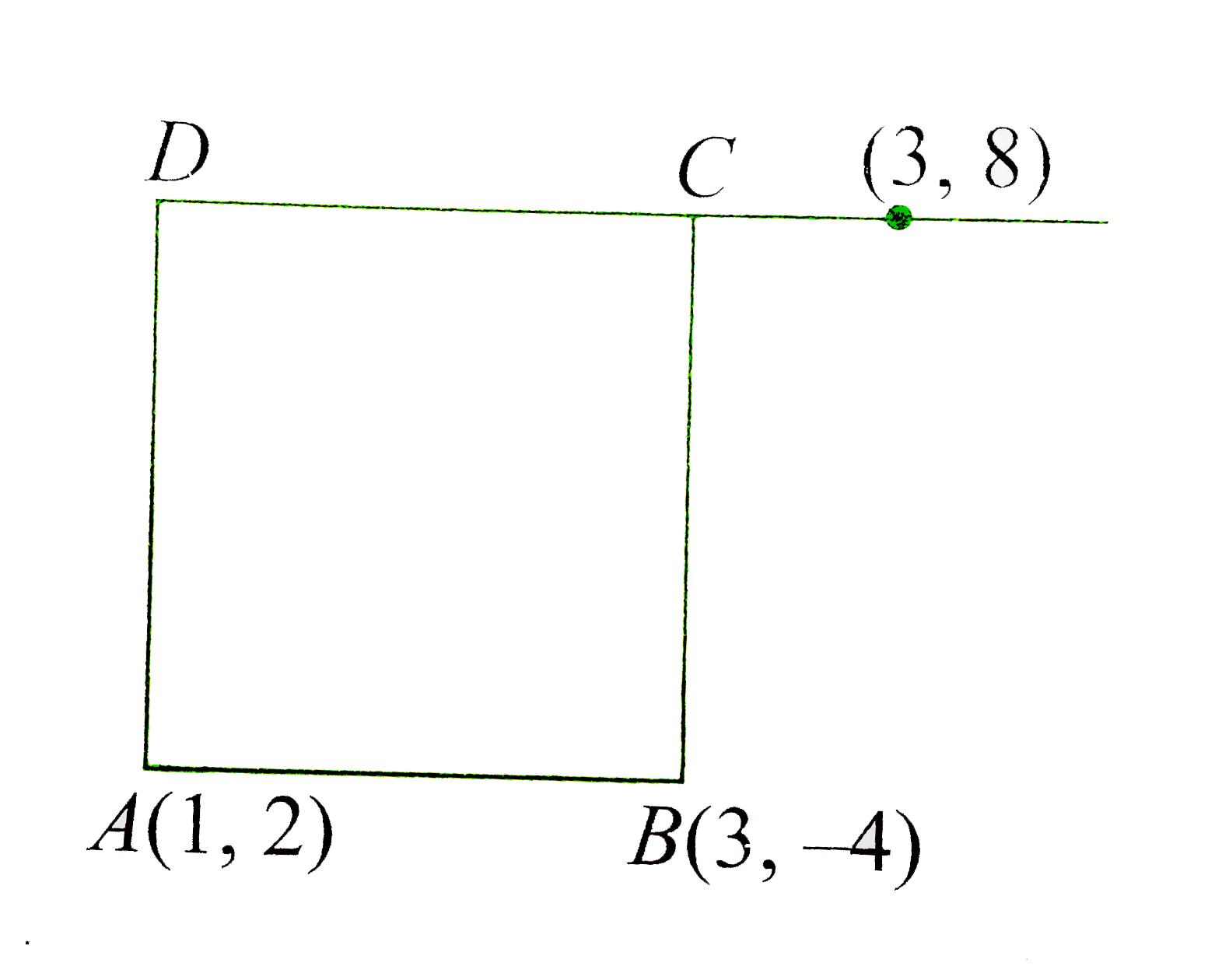
mAB=−4−23−1=−3
Thus, the equation of CD is y-8
=-3(x-3), i.e., y+3x=17. The equation of the right bisector of AB is
y+1=13(x−2)
or 3y=x-5
Solving it with line CD, we get x=28/5, y=1/5. Thus, the midpoint of CD is (28/5,1/5).
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)30videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)27videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.65videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year9videos
THEORY OF EQUATIONS
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
06:26View SolutionLet L be the line belonging to the family of straight lines (a+2b) x+(a-3b)y+a-8b =0, a, b ∈R, which is the farthest from the point (2, 2).
Area enclosed by the line L and the coordinate axes is03:31View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
01:30View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
01:26View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
03:35View SolutionABCD is a square A≡(1,2),B≡(3,−4). If line CD passes through (3,8), then the midpoint of CD is (a) (2,6) (b) (6,2) (c) (2,5) (d) (285,15)
03:29View SolutionABCD is a trapezium with AB∣∣DC . A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
01:37View SolutionABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P as shown in Figure. Prove that ar (ABP)=ar (Qua..ABCD).
01:27View SolutionIf ab=bc=cd, thenb3+c3+d3a3+b3+c3 will be equal to ab b. bc c. cd d. da
02:29View SolutionFind the values of a,b,c and d, if 3[abcd]=[a6−12d]+[4a+bc+d3].
03:02View Solutionसिद्ध कीजिये की बिंदु A(1,2),B(5,4),C(3,8) तथा D(−1,6) एक वर्ग शीर्ष है|
05:12View SolutionA (-2,-1) , B (1,0), C (4,3) and D (1,2) are the vertices of
□ ABCD then
Using midpoint formula , find the coordinates of midpoints of
join of B and D .05:32View SolutionLet A={1,2},B={1,2,3},c={5,6}andd={5,6,7} verify that
A×C is a subset of B×D03:00View SolutionLet A={1,2},B={1,2,3},c={5,6}andd={5,6,7} verify that
A×C is a subset of B×D02:33View SolutionFind the values of a,b,c and d, if 3[abcd]=[a6−12d]+[4a+bc+d3].
03:11View SolutionABCD is a square A≡(1,2),B≡(3,−4). If line CD passes through (3,8), then the midpoint of CD is (a) (2, 6) (b) (6,2) (c) (2,5) (d) (285,15)
04:04View Solution

