If (x,y) is a variable point on the line y=2x lying between the lines 2(x+1)+y=0 and x+3(y−1)=0 , then x∈(−12,67) (b) x∈(−12,37) y∈(−1,37) (d) y∈(−1,67)Solution in Tamil
x∈(−1/2,6/7)
x∈(−1/2,3/7)
y∈(−1,3/7)
y∈(−1,6/7)
The correct Answer is:B, D
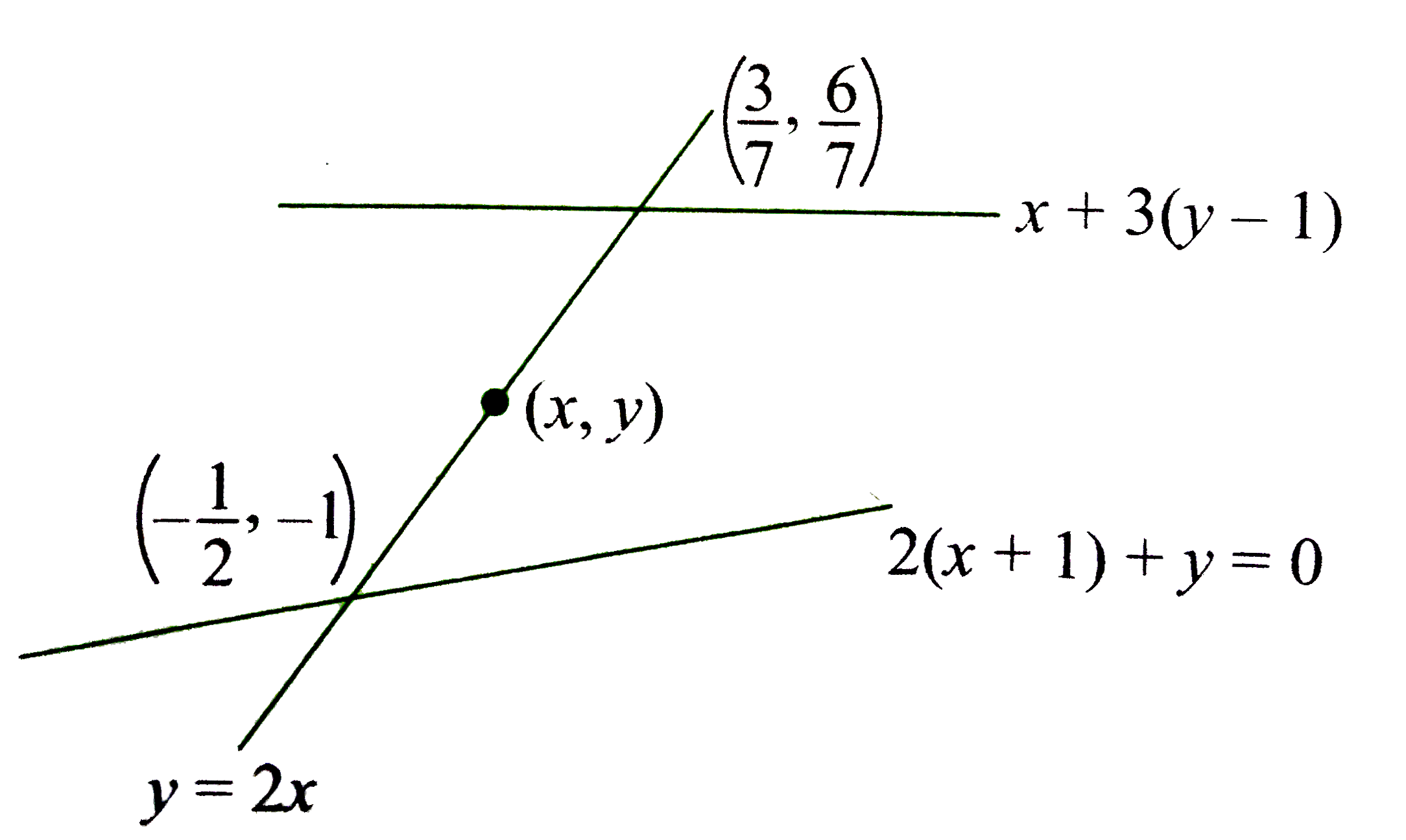
Solving y=2x, 2(x+1) + y = 0, we get x = -1/2, y=-1. Solving y=2x, x+3(y-1)=0, we get x=3/7, y=6/7.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)27videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Matrix)8videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Single)82videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year9videos
THEORY OF EQUATIONS
Similar Questions
Let L be the line belonging to the family of straight lines (a+2b) x+(a-3b)y+a-8b =0, a, b ∈R, which is the farthest from the point (2, 2).
Area enclosed by the line L and the coordinate axes is02:15View SolutionConsider the lines represented by equation (x2+xy−x)×(x−y)=0 forming a triangle. Then match the following lists:
 03:16View Solution
03:16View SolutionFind the equations of the diagonals of the square formed by the lines x=o,y=0,x=1andy=1.
05:16View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
01:11View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
02:03View SolutionIf (x,y) is a variable point on the line y=2x lying between the lines 2(x+1)+y=0 and x+3(y−1)=0 , then (a) x∈(−12,67) (b) x∈(−12,37) (c) y∈(−1,37) (d) y∈(−1,67)
03:54View SolutionThe equation of the plane through the line x+y+z+3=0=2x−y+3z+1 and parallel to the line x1=y2=z3 is a.x−5y+3=7 b. x−5y+3z=7 c. x+5y=3z=7 d. x+5y+3z=−7
03:20View SolutionThe image of line 2x+y=1 in line x+y+2=0 is : (A) x+2y−7=0 (B) 2x+y−7=0 (C) x+2y+7=0 (D) 2x+y+7=0
04:47View Solution1x+1y=7,
2x+3y=17(x≠0,y≠0) .07:27View SolutionIf x+y=7,x-y=1 then 2x =………..
06:03View SolutionColumn A0<x<yColumn B71x−1y7x−y
04:04View SolutionThe equation of the line passing through the point of intersection of the lines 2x+y+1=0,x−y−7=0 and the point (3, -2) is
03:13View Solution(x, y), (1, 2) ಮತ್ತು (7, 0) ಬಿಂದುಗಳು ಸರಳರೇಖಾಗತವಾಗಿದ್ದರೆ, x ಮತ್ತು y ಗಳ ನಡುವೆ ಒಂದು ಸಂಬಂಧವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
05:37View Solution(x,y),(1,2) ಮತ್ತು(7,0) x ಮತ್ತುy ಬಿಂದುಗಳಿಂದ ಉಂಟಾಗುವ ರೇಖಾಖಂಡವನ್ನು ವಿಭಾಗಿಸುವ ಅನುಪಾತವನ್ನು ನಿರ್ಧರಿಸಿ.
03:13View SolutionThe angles between the lines x+1−3=y−32=z+21 and x=y−7−3=z+72 are
05:05View SolutionIf (x,y) is a variable point on the line y=2x lying between the lines 2(x+1)+y=0 and x+3(y−1)=0 , then (a) x∈(−12,67) (b) x∈(−12,37) (c) y∈(−1,37) (d) y∈(−1,67)
05:31View Solution

