Let P(sinθ,cosθ) (0≤θ≤2π) be a point and let OAB be a triangle with vertices (0,0),(√32,0)and(0,√32) Find θ if P lies inside △OABSolution in Tamil
0<θ<π/12
5π/2<θ<π/2
0<θ<5π/2
5π/2<θ<π
The correct Answer is:A, B
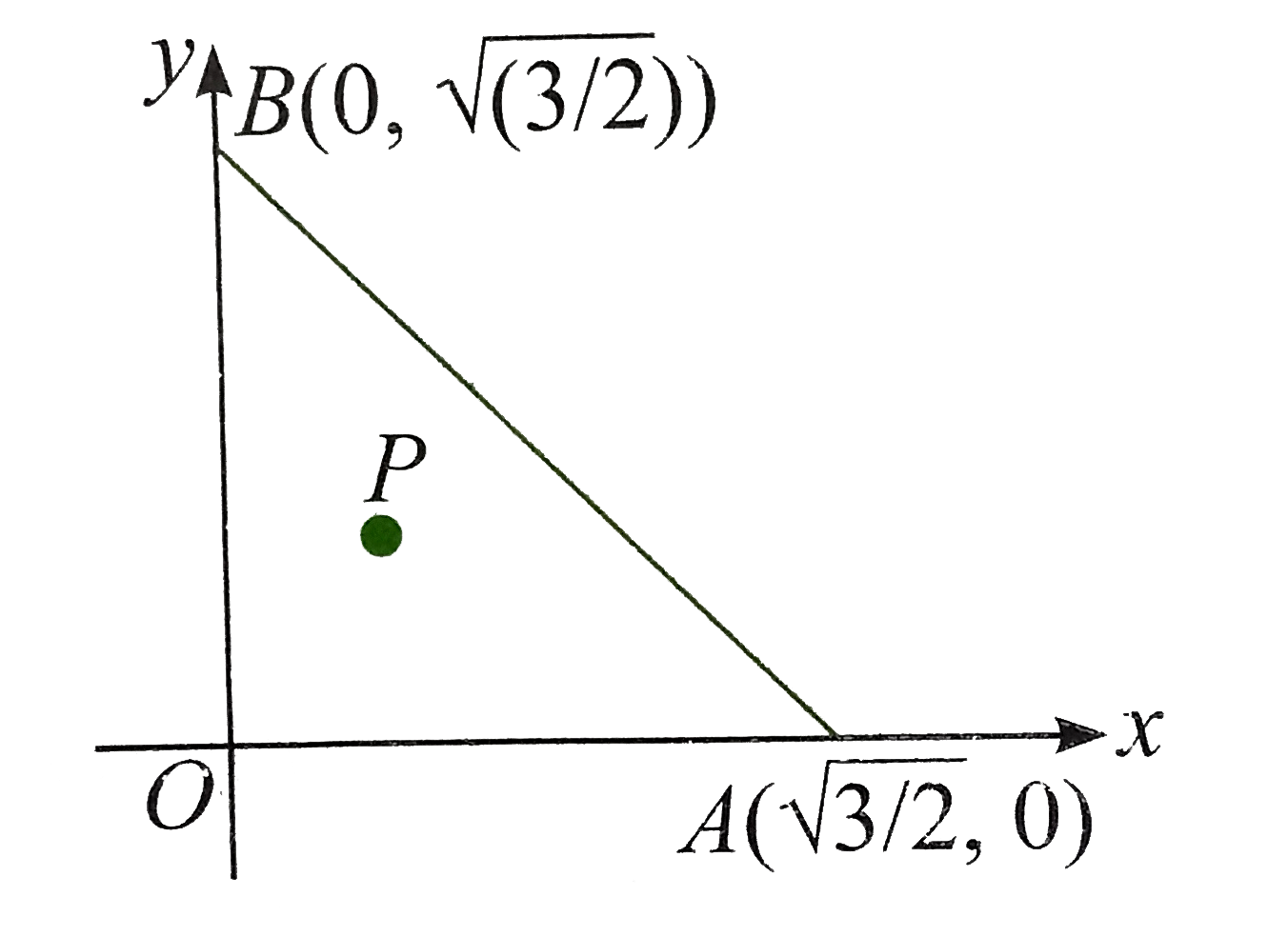
The equations of lines along OA, OB and AB are y=0, x=0, and x+y =√3/2, respectively.
Now, P and B will lie on the same side of y=0 if cosθ>0. Similarly, P and A will lie on the same side of x=0 if sin θ>0, and P and O will lie on the same side of x+y=√3/2 if sin θ+cosθ<√3/2. Hence, P will lie inside ΔABCif sinθ>0,cos θ>0, and sin θ+cos θ<√3/2, Now,
sin θ+cos θ<√32
or sin(θ+π4)<√34
Since sin θ>0 and cos θ>0,0<θ<π/12 or 5π/12<θ<π/2.
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)
27 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Matrix)
8 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Single)
82 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
Let L be the line belonging to the family of straight lines (a+2b) x+(a-3b)y+a-8b =0, a, b ∈R, which is the farthest from the point (2, 2).
Area enclosed by the line L and the coordinate axes is
View SolutionConsider the lines represented by equation (x2+xy−x)×(x−y)=0 forming a triangle. Then match the following lists:

View SolutionFind the equations of the diagonals of the square formed by the lines x=o,y=0,x=1andy=1.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View SolutionLet P(sin theta,cos theta)(0<=theta<=2 pi) be a point and let OAB be a triangle with vertices (0,0),(sqrt((3)/(2)),0) and (0,sqrt((3)/(2))) Find theta if P lies inside /_OAB
View SolutionLet P(sin theta,cos theta)(theta belongs to 0 to 2 pi) be apoint and OAB be a triangle with vertices (0,0),(sqrt((3)/(2)),0) and (0,sqrt((3)/(2)),0). Find theta if P lies inside the AQAB.
View SolutionGiven rsinθ=√3,r+4sinθ=2(√3+1) where 0≤θ≤2π
Value of θ will be-
View SolutionIf r sin theta = sqrt(3), r + 4 sin theta = 2(sqrt(3)+1), 0 le theta le 2pi , then theta =
View SolutionSolve (0∘≤θ≤360∘) :
(ii) cosθ+√3sinθ=2
View SolutionFor θ∈[0,2π] , consider the following statement :
p:√1−cos(2θ)=√2|sinθ|
q:√1−cos(2θ)+√2sinθ=0 if π≤θ≤2π
Then truth values of p and q are respectively:
View SolutionLet
Δ(θ)=∣∣ ∣∣1sinθ1sinθ1sinθ−1−sinθ1∣∣ ∣∣,0≤θ≤2π
solution of Δ(θ)=3 is
View SolutionLet Δ=∣∣ ∣∣1sinθ1−sinθ1sinθ−1−sinθ1∣∣ ∣∣0,≤θ≤2π. The
View SolutionLet P (sin theta, cos theta) (0 le theta le 2pi) be a point and let OAB be a triangle with vertices (0,0) , (sqrt(3/2),0) and (0,sqrt(3/2)) Find theta if P lies inside triangle OAB.
View SolutionLet P(sinθ,cosθ) (0≤θ≤2π) be a point and let OAB be a triangle with vertices (0,0),(√32,0)and(0,√32) Find θ if P lies inside △OAB
View Solution
