Question

Draw the graph of $y=x+\frac{1}{x}$.

Explanation

`y=2x^(2)-1` is an upward parabola having vertex at (0,-1).
It meets the x-axis at `(+-sqrt0)`
For `f(x)=cos^(-1)(2x^(2)-1)`to get defined.
`-1le2x^(2)-1le1`
`or" "0le2x^(2)le2`
`or" "0lex^(2)le1`
`or" "-1lexle1`
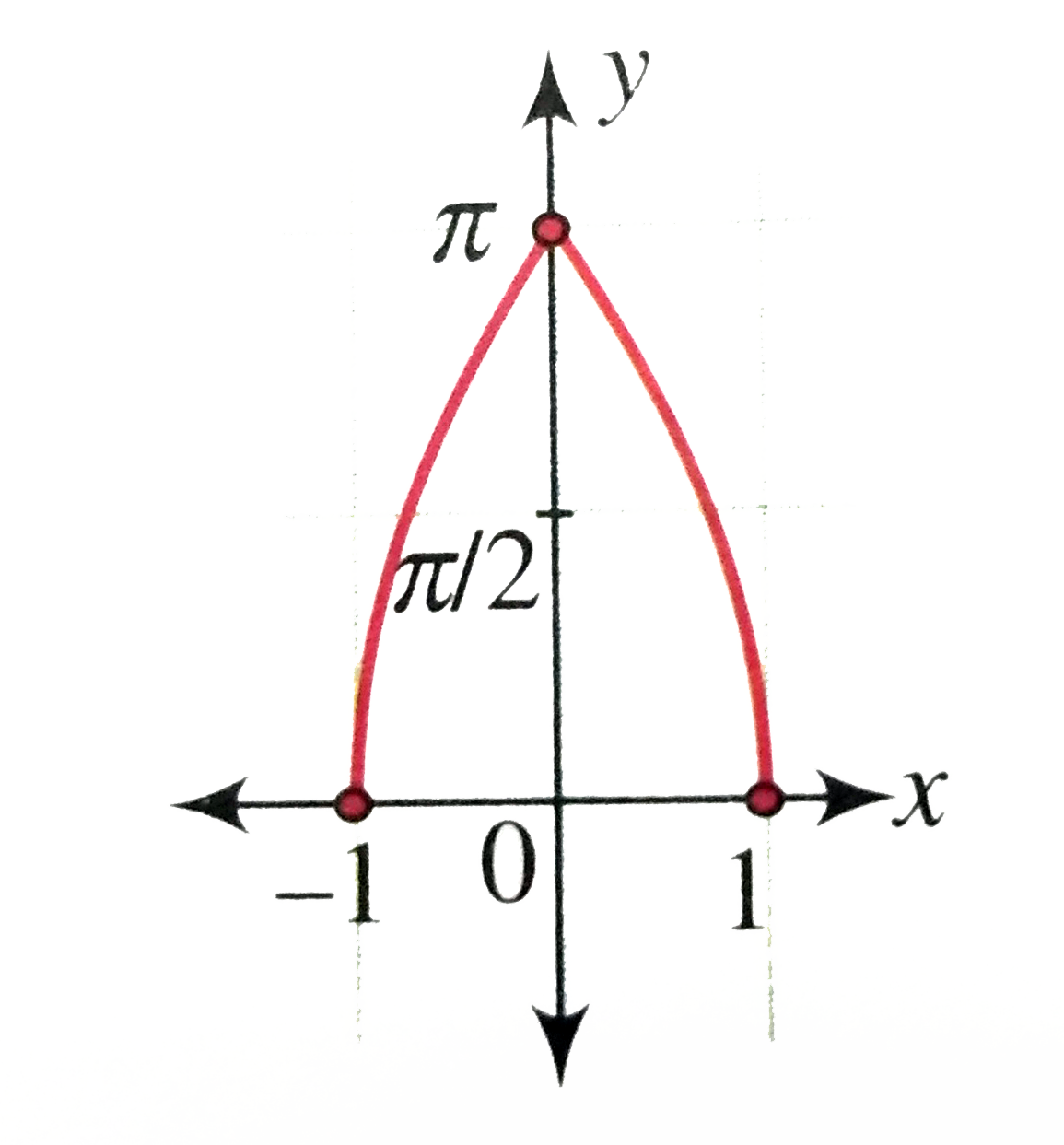
Hence the domain of `y=f(x) is [-1,1]`
`Now f(-1)=f(1)=cos^(-1)=0" and "f(0)=cos^(-1)(-1)=pi`
So the inportant points of the graph paper are as follows.

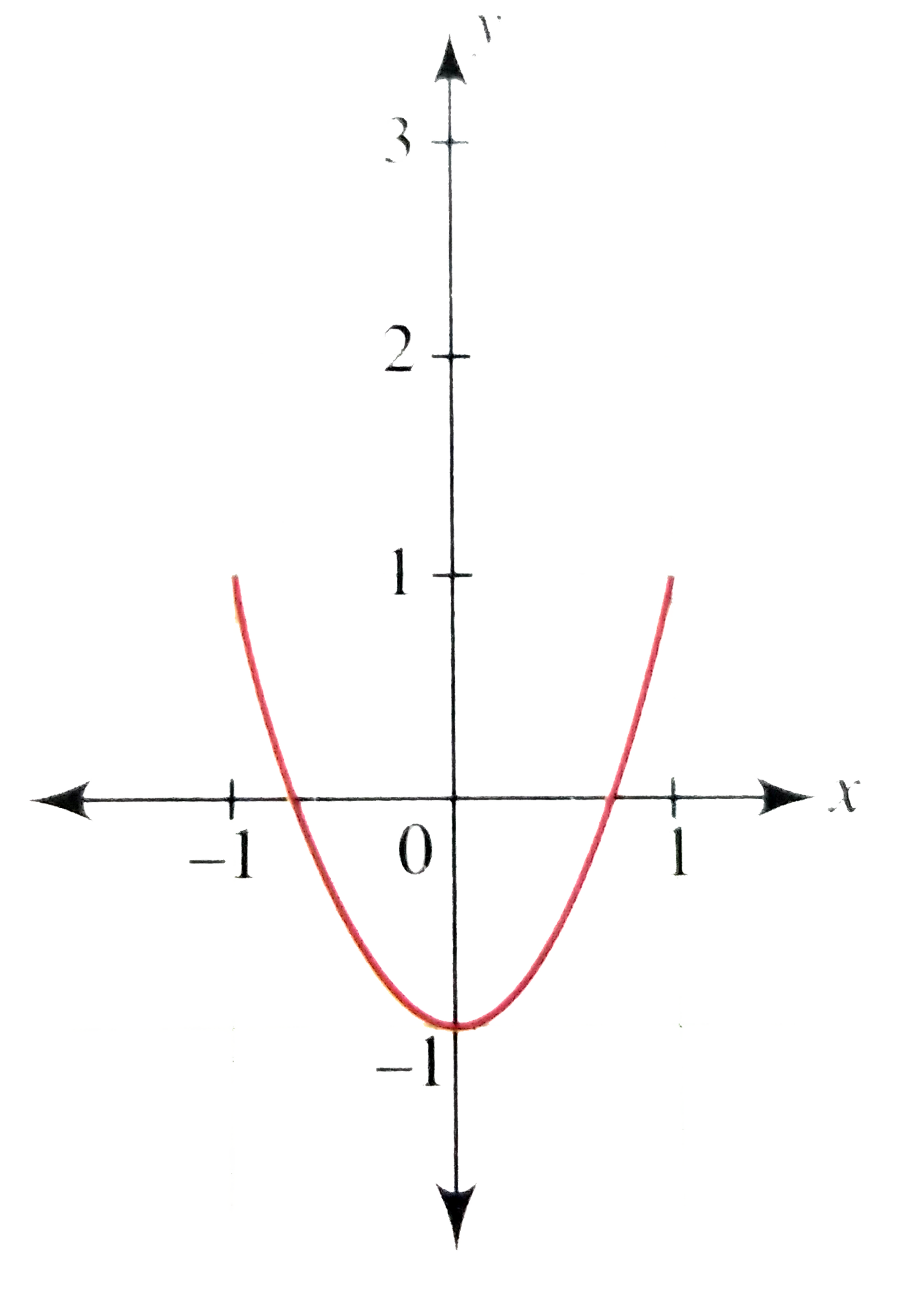
`"Now "f'(x)=(4x)/(sqrt(1-(2x^(2)-1))^(2))`
Clearly f'(x) does not exist at x=0, heance f(x) is non-differenctiable at x=0
`" Also "f'(x)gt0 "for x in [-1,0]`
`"and "f'(x)lt0 for x in (0, 1]`.
Hence the graph of `y=cos^(-1)(2x^(2)-1)` can be drawn as follows.