Let O be the circumcentre and H be the orthocentre of an acute angled triangle ABC. If A>B>C, then show that Ar(ΔBOH)=Ar(ΔAOH)+Ar(ΔCOH)Solution in Tamil

From the figure, we have
∠OAH=A−2(90∘−B)=B−C
Similarly, ∠OBH=A−C
and ∠OCH=A−B
Also, AH=2RcosA,BH=2RcosB,CH=2RcosC
Ar(ΔAOH)=12(R)(2RcosA)sin(B−C)
=R2cos(B+C)sin(C−B)
=R22(sin2C−sin2B)
Similarly, Ar(ΔBOH)=R22(sin2C−sin2A)
and Ar(ΔCOH)=R22(sin2B−sin2A)
Clearly, AR(ΔAOH)+Ar(ΔCOH)=Ar(ΔBOH)
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.112videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.28videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )1videos
PROGRESSION AND SERIES
- BOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank15videos
PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCE
Similar Questions
Find the value of a2+b2+c2R2 in any right-angled triangle.
09:31View SolutionIf the sides of a triangle are a, b and √a2+ab+b2, then find the greatest angle
02:44View SolutionIt is given that in a group of 4 students, the probability of 2 students not having the same birthday is 0.893. What is the probability that the 2 students have the same birthday?
View SolutionThe area of a right triangle is 6864 sq. units. If the ratio of its legs is 143:24, then the value of r is ______
04:32View SolutionIn Delta ABC,AD and BE are altitudes.Prove that (ar(Delta DEC))/(ar(Delta ABC))=(DC^(2))/(AC^(2))
03:04View Solutionकिसी त्रिभुज ABC की मधिकाएँ CD और BE एक दूसरे को O पर कटती है , तो अनुपात Ar △ODE:Ar △ABC किसके बराबर होगा ?
04:47View SolutionLet O be the circumcentre and H be the orthocentre of an acute angled triangle ABC. If A>B>C, then show that Ar(ΔBOH)=Ar(ΔAOH)+Ar(ΔCOH)
03:29View SolutionIt is given that ΔABC~ΔPRQandBCQR=23 then ar(ΔPQR)ar(ΔABC)=?
07:20View SolutionIn an equilateral ΔABC,D is the midpoint of AB and E is the midpoint of AC. Then, ar(ΔABC):ar(ΔADE)=?
 02:51View Solution
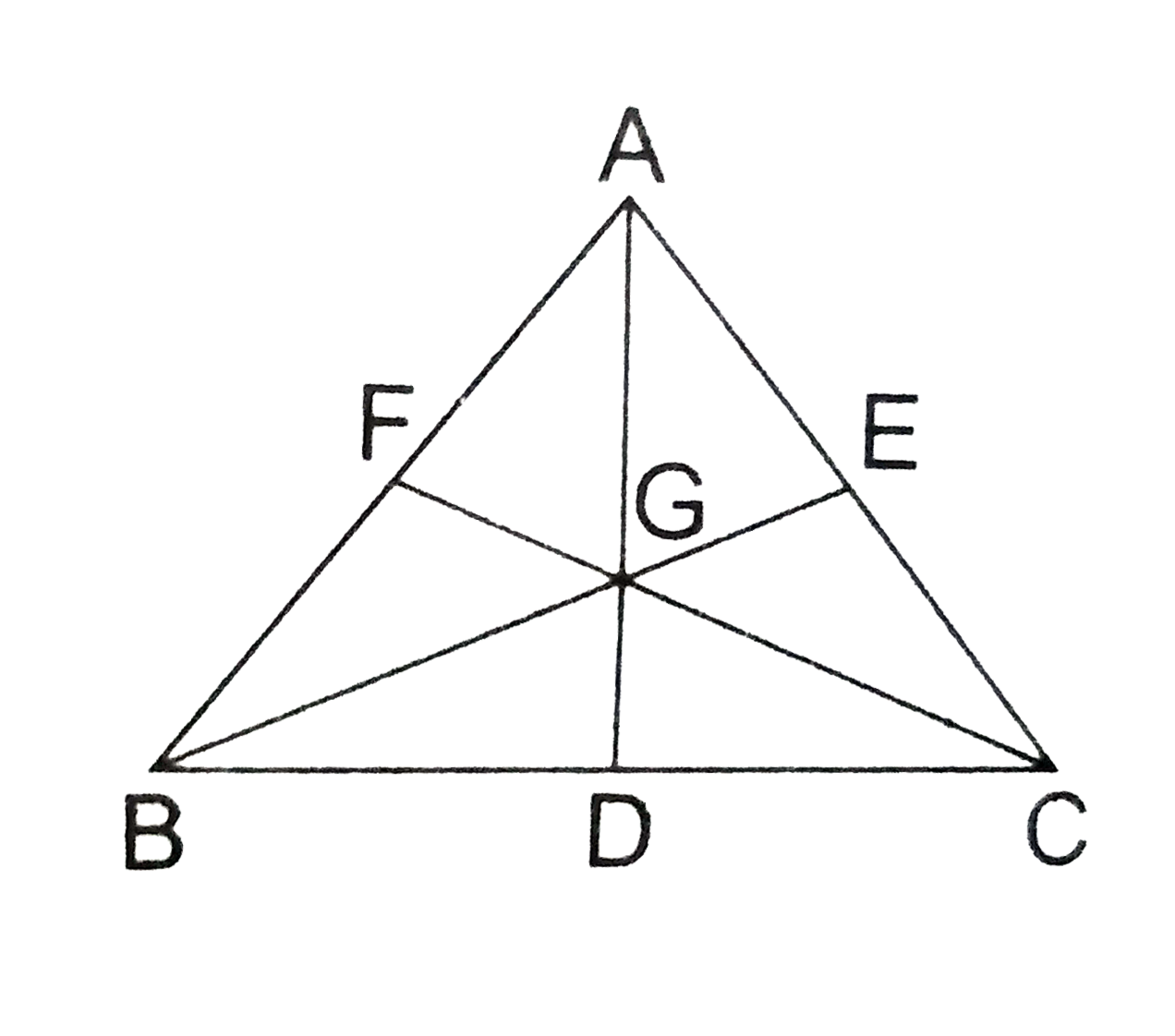
02:51View SolutionIf the medians of a △ABC intersect at G, show that
ar(△AGB)=ar(△AGC)=ar(△BGC)
=13ar(△ABC).
 01:33View Solution
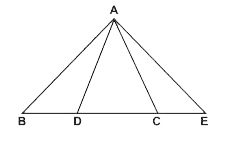
01:33View SolutionIn the given figure ar (ΔABC)= ar (ΔADE). AC is the median of ΔADE. If ar (ACE) =14cm2 then ar (ΔABC) = ?
 03:23View Solution
03:23View SolutionIts vertices A, B, C and D are joined by a point O located in the interior of a rectangle ABCD. Prove that ar ( Delta AOD ) + ar ( Delta BOC ) = ar ( Delta AOB ) +ar(Delta COD )
02:22View SolutionDelta ABC A point D on BC is such that BD = ( 1)/( 3) DC Show that ar( Delta ABD ) = ( 1)/( 4) ar ( Delta ABC )
06:03View SolutionIf ΔABC~ΔPQR with BCQR=13, then find arΔPRQarΔBCA ?
06:00View SolutionΔABC and ΔBDC are on the same base BC. Prove that ar(ΔABC)ar(ΔDBC)=AODO
 04:25View Solution
04:25View Solution

