Doubtnut Promotions Sticky

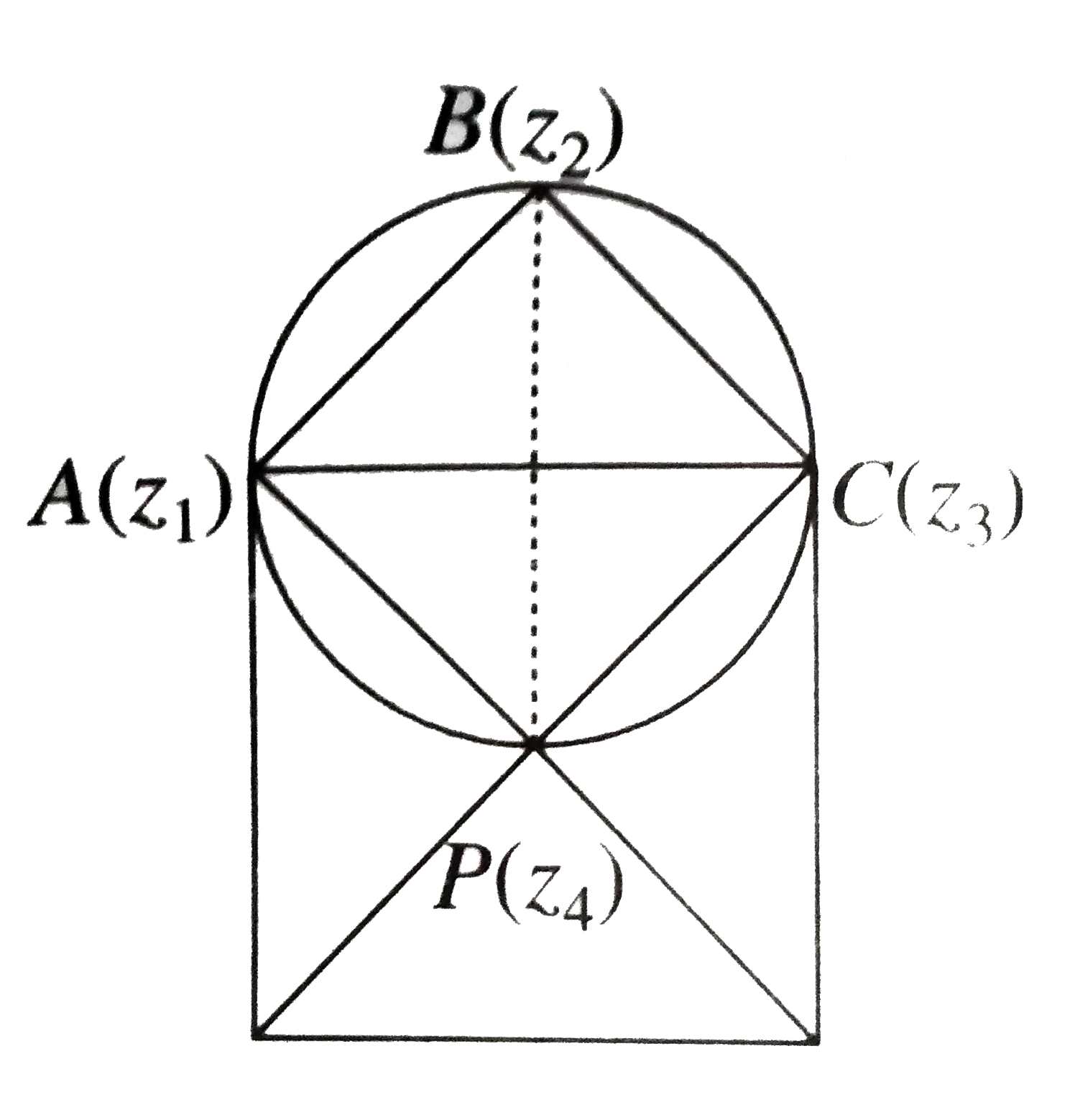
Let z1, z2, z3 are the vertices of ΔABC, respectively, such that z3−z2z1−z2 is purely imaginery number. A square on side AC is drawn outwardly. P(z4) is the centre of square, then

A

|z1−z2|=|z2−z4|

B

arg(z1−z2z4−z2)+arg(z3−z2z4−z2)=+π2

C

arg(z1−z2z4−z2)+arg(z3−z2z4−z2)=0

D

z1, z2, z3 and z4 lie on a circle

Text Solution
Verified by Experts

The correct Answer is:C, D

(c,d) P is centre of square ⇒AP=PC and ∠APC=π2
∠ABC is also π2.
⇒ABCP is cyclic quadrilateral
⇒A,B,C,P lie on a circle.
⇒ In circl chord, AP=PC
⇒ arc AP= are PC
⇒∠ABP=∠PBC
⇒BP is angular bisector.
Let arg(z1−z2z4−z2)=−α........(i)
⇒arg(z3−z2z4−z2)=α..........(ii)
Add (i) and (ii), arg(z1+z2z4−z2)+arg(z3−z2z4−z2)=0
ocr_image

Doubtnut Promotions Banner
|
Updated on:21/07/2023
Class 12MATHSCOMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Let A(z1),B(z2),C(z3) be the vertices of an equilateral triangle ABC in the Argand plane, then the number z2−z32z1−z2−z3, is

    Apurely real
    Bpurely imaginary
    Ca complex number with non-zero and imaginary parts
    Dnone of these
  • Question 2 - Select One

    Let z1,z2,z3,z4 are distinct complex numbers satisfying |z|=1 and 4z3=3(z1+z2), then |z1−z2| is equal to

    A1 or i
    Bior−i
    C1 or i
    Dior−1