Three vertices are chosen randomly from the seven vertices of a regular 7-sided polygon. The probability that they form the vertices of an isosceles triangle isSolution in Tamil
17
13
37
35
The correct Answer is:D
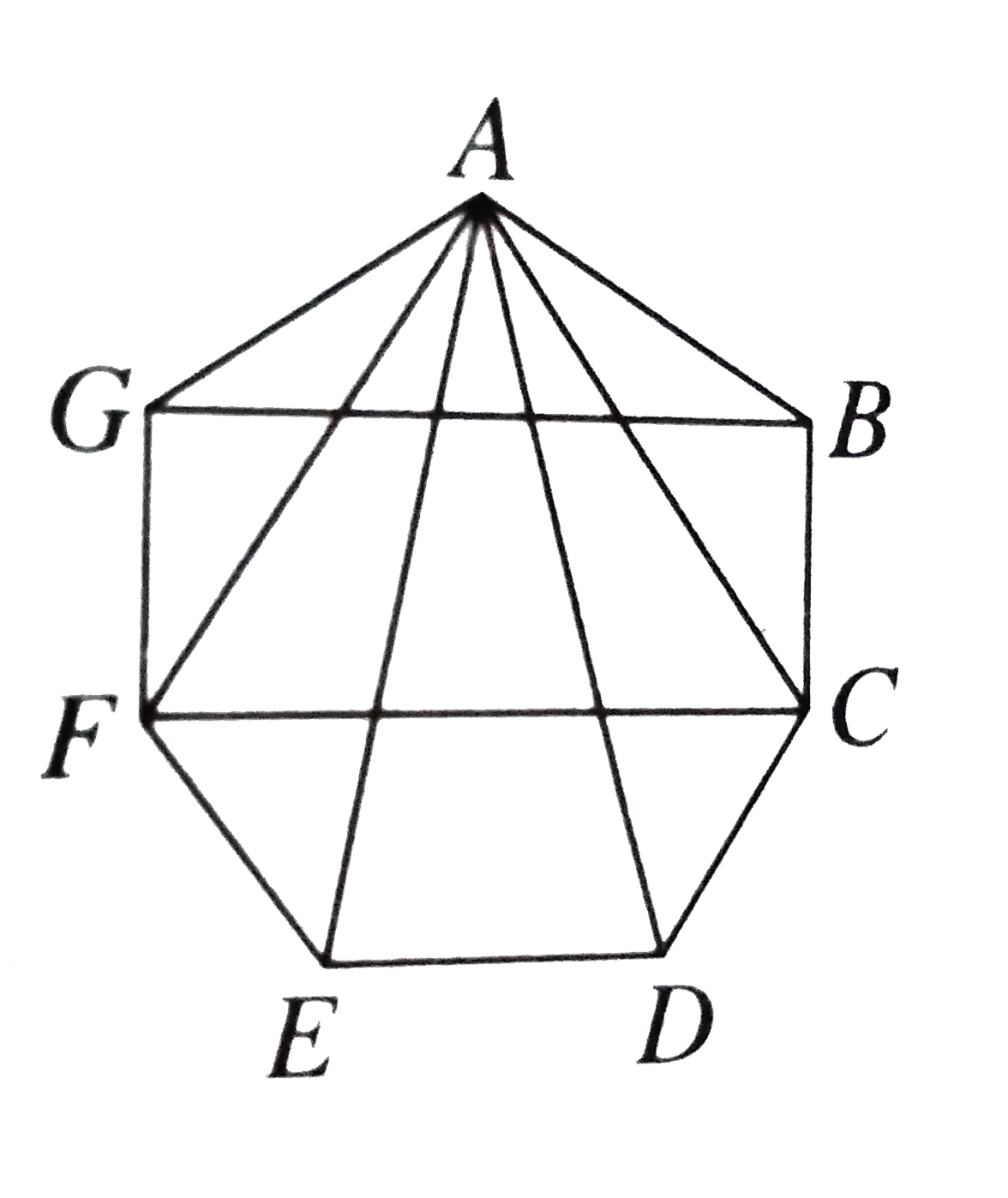
(d) ΔAGB, ΔAFC and ΔAED are isosceles
∴P=7C1×3'7C3=7×37×6×53×2=35
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - PROBABILITYEXERCISE - Comprehension2videos
PROBABILITY
- BOOK - CENGAGECHAPTER - PROBABILITYEXERCISE - Multiple Correct Answer13videos
PROBABILITY
- BOOK - CENGAGECHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - Exercise9videos
PRINCIPLE OF MATHEMATICAL INDUCTION
- BOOK - CENGAGECHAPTER - PROBABILITY AND STATISTICSEXERCISE - Question Bank24videos
PROBABILITY AND STATISTICS
Similar Questions
A slip of paper is given to a person A who marks it either with a plus sign or a minus sign. The probability of his writing a plus sign is 1/3. A passes the slip to B, who may either leave it alone or change the sign before passing it to C. Next C passes the slip to D after perhaps changing the sign. Finally D passes it to a refere after perhaps changing the sign. B,C,Deachchan≥thesignwithprobability2//3.<br>TheprobabilitytˆtherefereeobservesaplussignontheslipifitisknowntˆA wrote a plus sign is
08:45View SolutionThe probablities of events , A∩B, A, B and A∪B are respectively in A.P. with second term equal to the common difference. Therefore A and B are
01:43View SolutionProve that by using the principle of mathematical induction for all n∈N:
1.3+3.5+5.7+....+(2n−1)(2n+1)=n(4n2+6n−1)303:27View SolutionIf two events A and B are such that P(Al)=0.3, P(B)=0.4 and P(A∩Bl)=0.5, then P(BA∪Bl) equals
02:38View SolutionThree distinct vertices are chosen at random from the vertices of a given regular polygon of (2n + 1) sides Let all such choices are equally likely and the probability that the centre of the given polygon lies in the interior of the triangle determined by these three chosen random points is 5/14 Three vertices of the polygon are chosen at random. The probability that these vertices form an isosceles triangle is.
04:34View SolutionThree vertices are chosen from the vertices of a regular hexagon, then the probability that they will form an equilateral triangle is
04:27View SolutionThree vertices are chosen randomly from the seven vertices of a regular 7-sided polygon. The probability that they from the vertices of an isosceles triangle is-
02:43View SolutionThree vertices are chosen randomly from the seven vertices of a regular 7-sided polygon. The probability that they form the vertices of an isosceles triangle is
05:03View SolutionThree vertices are chosen at random from the vertices of a regular hexagon then the probability that the triangle with these vertices is an equilateral triangle is equal to
03:36View SolutionThree vertices are chosen at random from the vertices of a regular hexagon then
The probability that the triangle has exactly one side common with the side of the hexagon is02:39View SolutionThree vertices are chosen at random from the vertices of a regular hexagon then
The probability that the triangle has exactly two sides common with the side of the hexagon is04:08View Solution3 out of 6 vertices of a regular hexagon are chosen at a time at random. The probability that the triangle formed with these three vertices is an equilateral triangle , is
03:36View Solutionकिसी समषटभुज के 6 शीर्षों में 3 शीर्षों को यदृच्छया चुना गया है। इन तीन शीर्षों से बनने वाले त्रिभुज समबाहु हो, तो इसकी प्रायिकता है
03:28View Solutionयदि एक सम षट्भुज के छः शीर्षो में से तीन यादृश्चिक चुने जाते है, तो इन चुने गए शीर्षो द्वारा बने त्रिभुज के समबहु होने की प्रायिकता है
03:36View SolutionThree distinct vertices are randomly chosen among the vertices of a cube. The probability that they from equilateral triangle is
04:16View Solutionएक समषट्भुज के छ: शीर्षों में से तीन शीर्षों को यादृच्छिक रूप से चुना जाता है। इन तीन शीर्ष से बने त्रिभुज का समबाहु होने की प्रायिकता है
02:39View Solution

