Let f(x)=max{1+sinx,1,1−cosx},x∈[0,2π],andg(x)=max{1,|x−1|},x∈R. Then (a)g(f(0))=1 (b) g(f(1))=1 (c)f(f(1))=1 (d) f(g(0))=1+sin1Solution in Tamil
g(f(0))=1
g(f(1))=1
f(f(1))=1
f(g(0))=1+sin1
The correct Answer is:A, B, D
f(0)=max{1+sin0,1,1−cos0}=1
g(0)=max{1,|0−1|}=1
f(1)=max[1+sin1,1,1−cos1}=1+sin1
g(f(0))=g(1)=max{1,|1−1|}=1
f(g(0))=f(1)=1+sin1
g(f(1))=g(1+sin1)=max{1,|1+sin1−1|}=1
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Comprehension)
32 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Matrix)
9 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Single)
125 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
28 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
Consider the functions
f(x)={x+1,x≤12x+1,1<x≤2andg(x)={x2,−1≤x<2x+2,2≤x≤3
The domain of the function f(g(x)) is
View SolutionThe function f(x) is defined on the interval [0, 1]. Now, match the following lists:
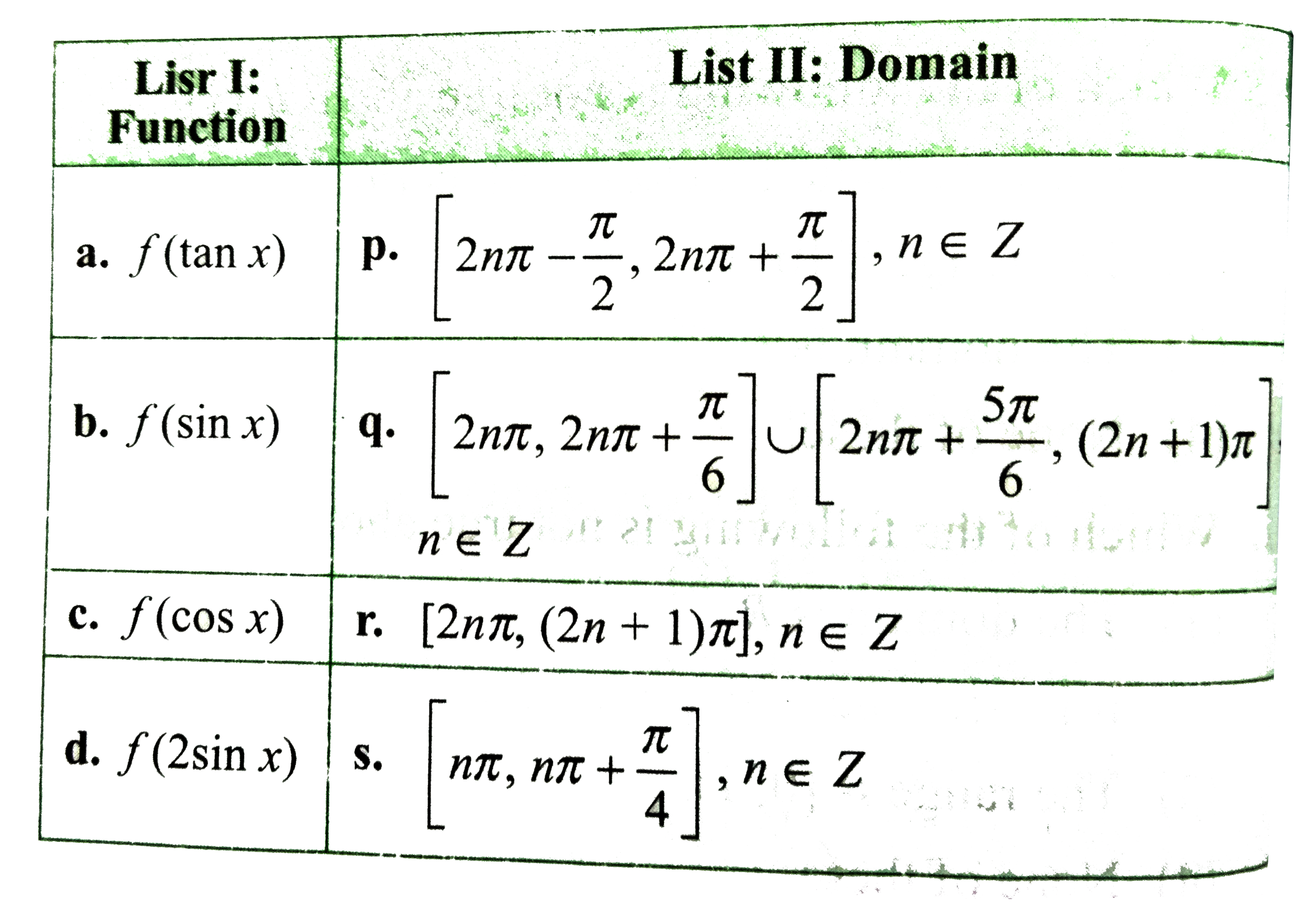
View SolutionThe relation R={(1,1),(2,2),(3,3),(1,2),(2,3),(1,3)} on a set A={1, 2, 3} is
View SolutionLet a,b,c,d be positive integers such that (log)ab=32and(log)cd=54. If (a−c)=9, then find the value of (b−d).
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj+ˆk and ˆi−ˆj+ˆk, in the order from right-handed system ∀x ∈R, is
View SolutionLet f(x)=max{1+sinx,1,1−cosx},x∈[0,2π],andg(x)=max{1,|x−1|},x∈R. Then (a)g(f(0))=1 (b) g(f(1))=1 (c)f(f(1))=1 (d) f(g(0))=1sin1
View SolutionLet g′(x)>0andf′(x)<0∀x∈R. Then (f(x+1))>g(f(x−1)) f(g(x−1))>f(g(x+1)) g(f(x+1))<g(f(x−1)) g(g(x+1))<g(g(x−1))<="" b="">
View Solutionlet ( f(x) = 1-|x| , |x| 1 ) g(x)=f(x+1)+f(x-1)
View SolutionSuppose that f(x) is differentiable invertible function f′(x)≠0andh′(x)=f(x). Given that f(1)=f′(1)=1,h(1)=0 and g(x) is inverse of f(x) . Let G(x)=x2g(x)−xh(g(x))∀x∈R. Which of the following is/are correct? G′(1)=2 b. G′(1)=3 c.G1=2 d. G1=3
View SolutionLet g(x)=1+x-[x] and f(x)=-1 if x 0, then f|g(x)]=1x>0
View SolutionLet f(x)={x-1,-1<=x<0 and x^(2),0<=x<=1,g(x)=sin x and h(x)=f(|g(x)|)+[f(g(x)) Then
View Solutionমনে করাে, f:R→R হল f(x)=−x3+x দ্বারা সংজ্ঞাত। g:[−1,1]→R,h:[−1,1]→R নিম্নরূপে সংজ্ঞাত। g(x)=min(f(x),0),h(x)=max(f(x),0) :g(x)=−12 সমীকরণের বীজসংখ্যা হয় -
View SolutionLet p (x) be a polynomial with real coefficient and p(x)=x2+2x+1. Find P (1).
View SolutionLet f(x)=max(1+s∈x,1,1−cosx),x∈[0,2π],andg(x)=max{1,|x−1|},x∈R. Then g(f(0))=1 (b) g(f(1))=1 f(f(1))=1 (d) f(g(0))=1+sin1
View SolutionSuppose that f(x) is differentiable invertible function f′(x)≠0andh′(x)=f(x). Given that f(1)=f′(1)=1,h(1)=0 and g(x) is inverse of f(x) . Let G(x)=x2g(x)−xh(g(x))∀x∈R. Which of the following is/are correct? G′(1)=2 b. G′(1)=3 c.G1=2 d. G1=3
View SolutionLet f (x) and g (x) be differentiable for 0 < x < 1 such f(0)= 0 , g (0) =0, f(1)=6. Let there exist a real number c in (0, 1) such that f’ (c) =2g’ (c), then the value of g (1) must be A) 1 B) 3 C) 2.5 D) -1
View Solution
