The figure illustrates the graph of the function $y = f (x)$ defined in [-3, 2].

Identify the correct statement(s)?

A

Range of $y = f (- | x |) is [- 2, 2]$

B

Domain of $y = f (| x |) is [- 2, 2]$

C

Domain of $y = f | x | + 1) is [- 1, 1]$

D

Range of $y = f (| x | + 1) is [- 1, 0]$

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

(1) Graph of $y = f (- | x |)$ is

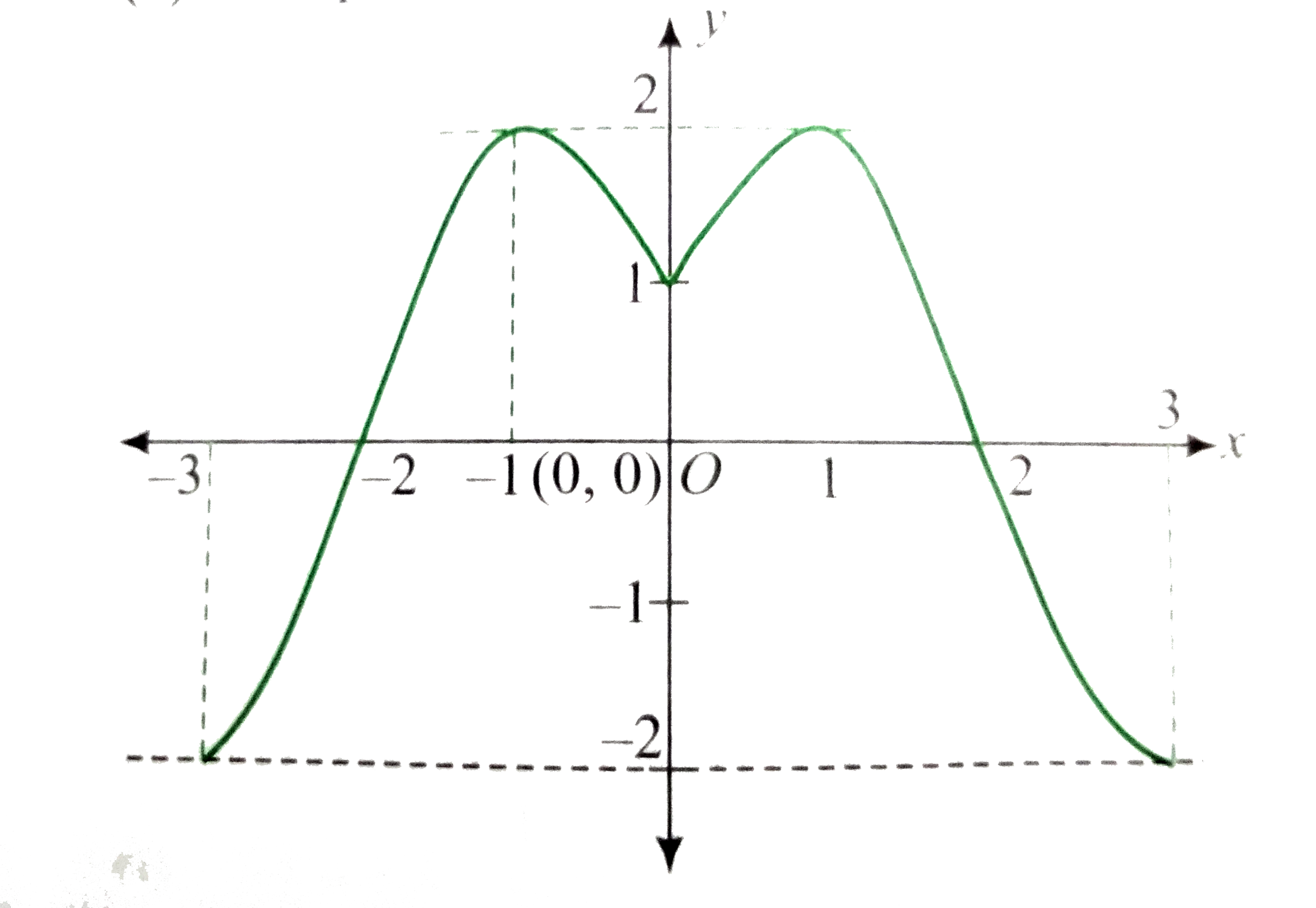
$∴$ range is [-2, 2]
(2) Domain of $y = f (| x |)$ is
$- 3 \leq | x | \leq 2$
$\Rightarrow - 2 \leq x \leq 2$
(3) Domain of $y = f (| x | + 1)$ is
$- 3 \leq | x | + 1 \leq 2$
$\Rightarrow - 4 \leq | x | \leq 1$
$\Rightarrow x \in [- 1, 1]$
(4) Graph of $y = f (| x | + 1)$ is

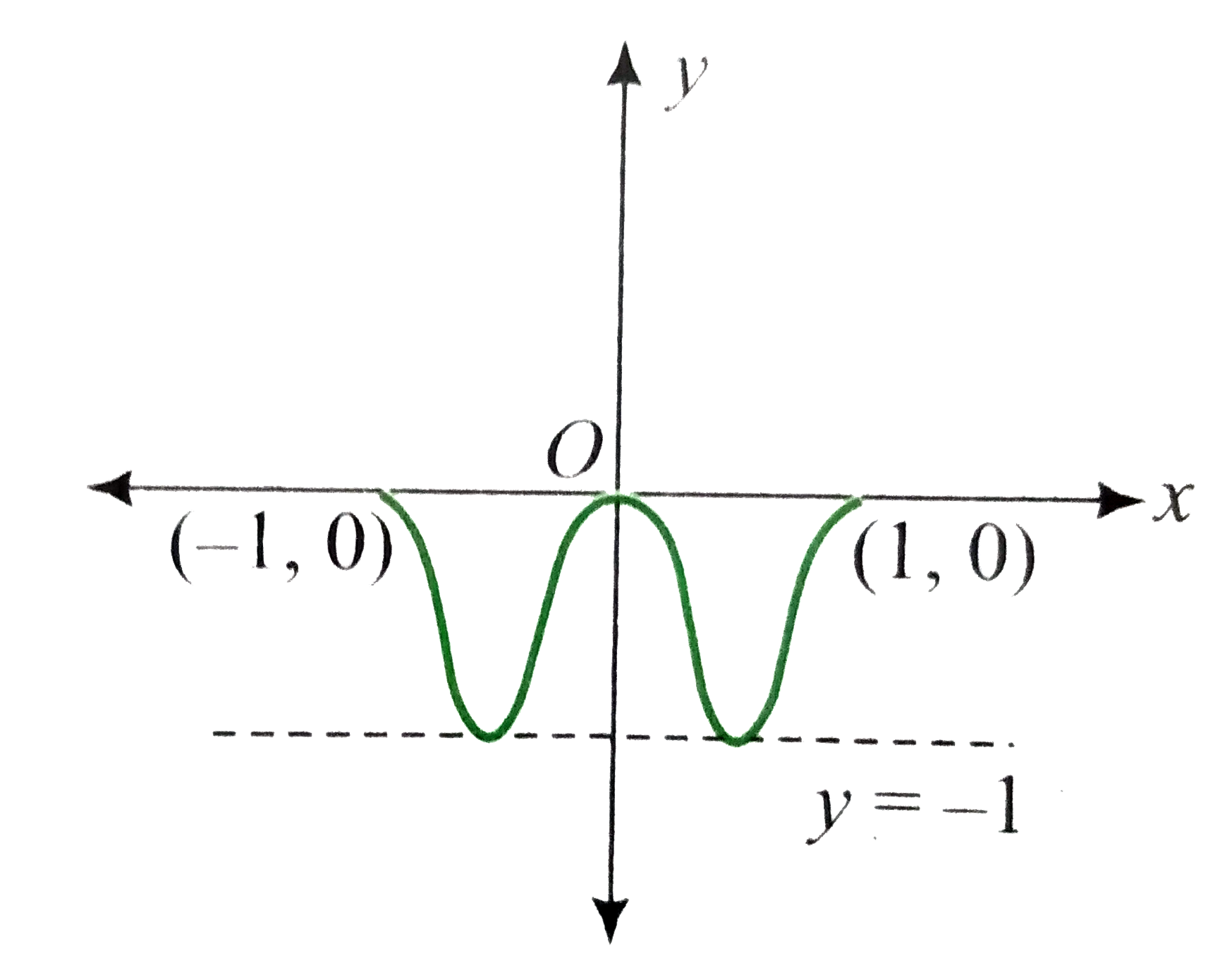
$∴$ Range is [-1, 0]

|

Updated on:21/07/2023

Class 12 MATHS RELATIONS AND FUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
If graph of a function $f (x)$ which is defined in [-1, 4] is shown in the following figure then identify the correct statement(s).

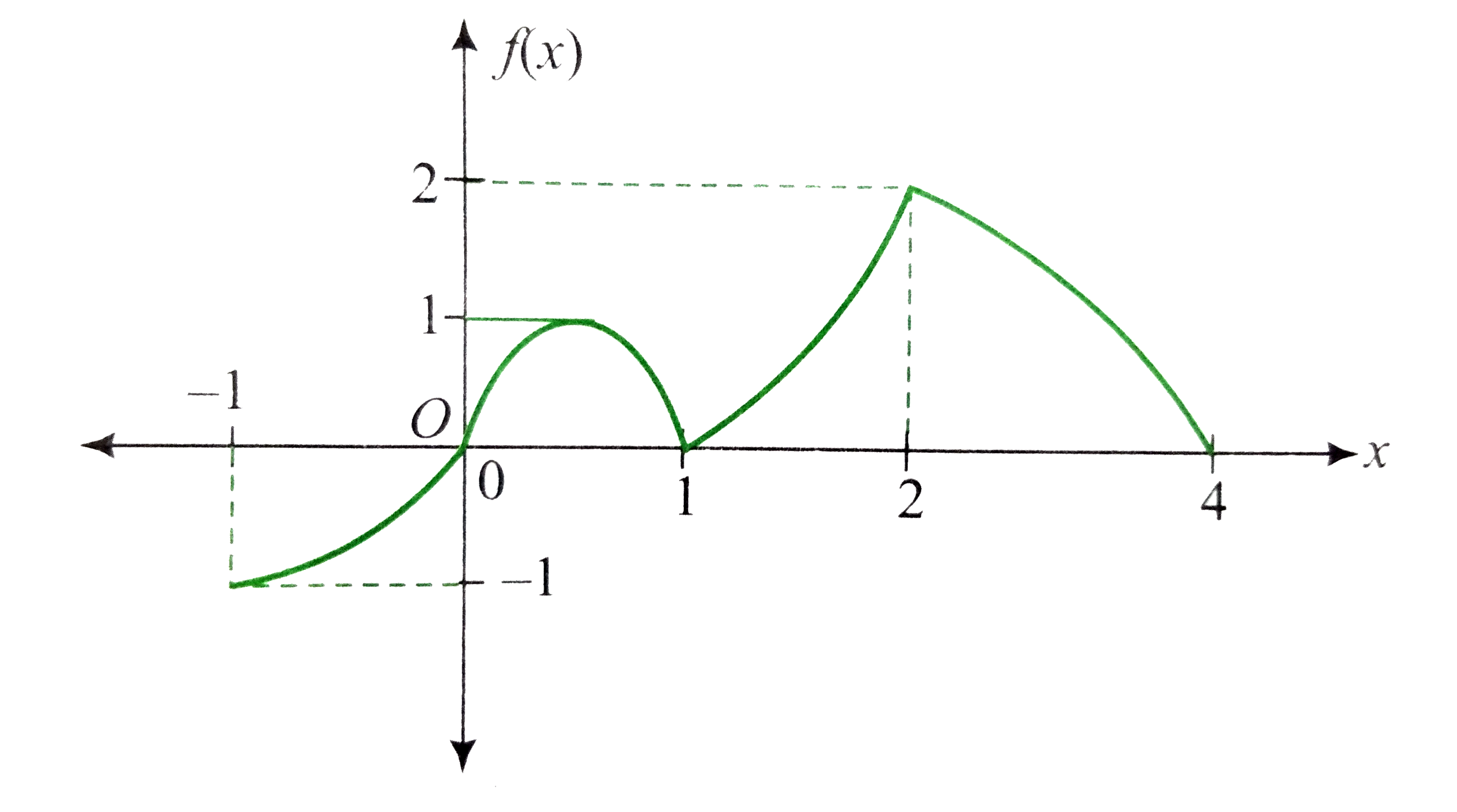Adomain of $f (| x | - 1) is [- 5, 5]$
Brange of $f (| x | + 1) is [0, 2]$
Crange of $f (- | x |) is [- 1, 0]$
Ddomain of $f (| x |) is [- 3, 3]$

CENGAGE-RELATIONS AND FUNCTIONS-Exercise (Multiple)

Home
Ask Doubt
Profile