Let f(x)=34x+1,fn(x)bedef∈eda^2(x)=f(f(x)),andforn≥2,fn+1(x)=f(fn(x)).Ifλ=(lim)n→∞fn(x) , then λ is independent of x λ is a linear polynomial in x the line y=λ has slope 0. the line 4y=λ touches the unit circle with centre at the origin.Solution in Tamil
λ is independent of x
λ is a linear polynomial in x
the line y=λ has slope 0
the line 4y=λ touches the unit circle with center at the origin.
The correct Answer is:A, C, D
f2(x)=f(34x+1)=34(34x+1)+1=(34)2x+34+1(1)
f3(x)=f{f2(x)}=34{f2(x)+1}
=34{(34)2x+34+1}+1
=(34)3x+(34)2+34+1
∴fn(x)=(34)nx+(34)n−1+(34)n−2+...+(34)+1
=(34)nx+1−(34)n1−34
∴λ=limn→∞fn(x)=0+4=4
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Comprehension)32videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Matrix)9videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Single)125videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank28videos
Quadratic Equations, Inequalities, Modulus and Logarithms
- BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
Similar Questions
Consider the functions
f(x)={x+1,x≤12x+1,1<x≤2andg(x)={x2,−1≤x<2x+2,2≤x≤3
The domain of the function f(g(x)) is06:51View SolutionThe function f(x) is defined on the interval [0, 1]. Now, match the following lists:
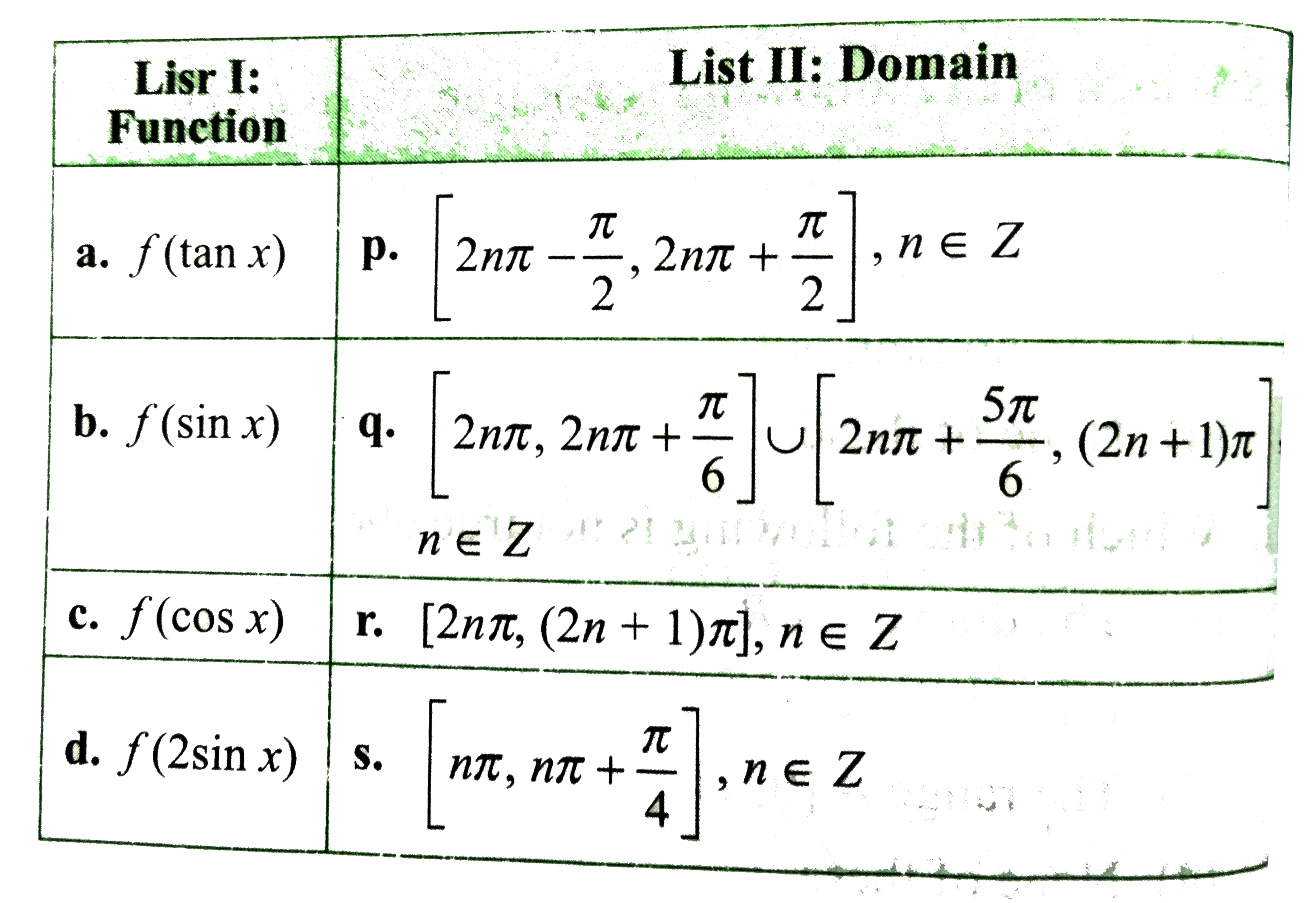 02:23View Solution
02:23View SolutionThe relation R={(1,1),(2,2),(3,3),(1,2),(2,3),(1,3)} on a set A={1, 2, 3} is
01:10View SolutionLet a,b,c,d be positive integers such that (log)ab=32and(log)cd=54. If (a−c)=9, then find the value of (b−d).
02:34View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj+ˆk and ˆi−ˆj+ˆk, in the order from right-handed system ∀x ∈R, is
02:34View SolutionLet f(x)=34x+1,fn(x) be defined as f2(x)=f(f(x)), and for n≥2,fn+1(x)=f(fn(x)). If λ=(lim)n→∞fn(x) , then (a)λ is independent of x (b)λ is a linear polynomial in x (c)the line y=λ has slope 0. (d)the line 4y=λ touches the unit circle with centre at the origin.
02:04View SolutionEvaluate ∫f(x) is polynomaial function of then the degree, prove that ∫exf(x)dx=ex[f(x)f'(x)+fx=fx+......+(−1)nfn(x)] where fn(x)dx+dnfdxn
02:02View SolutionIf f(x)=(a-x^(n))^((1)/(n)),a>0 and n in N, then prove that f(f(x))=x for all x.
02:47View SolutionIf f(x)=sum_(lambda=1)^(n)(x-(5)/(lambda))(x-(4)/(lambda+1)) then lim_(n rarr oo)f(0) is equal to
03:12View SolutionIf f(x)=sum_(lambda=1)^(n)(x-(5)/(lambda))(x-(4)/(lambda+1)) then lim_(n rarr oo)f(0) is equal to
02:17View SolutionIf f(x)=|[x+lambda,x,x] , [x,x+lambda,x] , [x,x,x+lambda]| then f(12x)-f(x)=
01:36View SolutionLet f(x) be a function satisfying f(x+y)=f(x)f(y) for all x,y∈N such that f(1) = 3 and n∑x=1f(x)=120 . Then the vlaue of n is :
03:07View SolutionLet f(x)>0 be a continuous function such that the area bounded by the curve y=f(x),x -axis and the lines x=0 and x=λ is +λ22+cos2λ .Then f(π4) is
07:33View SolutionLet f(x)=34x+1,fn(x) be defined as f2(x)=f(f(x)), and for n≥2,fn+1(x)=f(fn(x)). If λ=limn→∞fn(x), then
01:09View SolutionIf f(x)=(a−xn)1n,a>0andn∈N, then prove that f(f(x))=x for all x.
05:14View Solutionवक्तव्य I यदि ∫10esinxdx=λतब ∫2000esinxdx=200λ
वक्तव्य II ∫na0f(x)dx=n∫10f(x)dx,n∈Iतथा f(a+x)=f(x)View Solution

