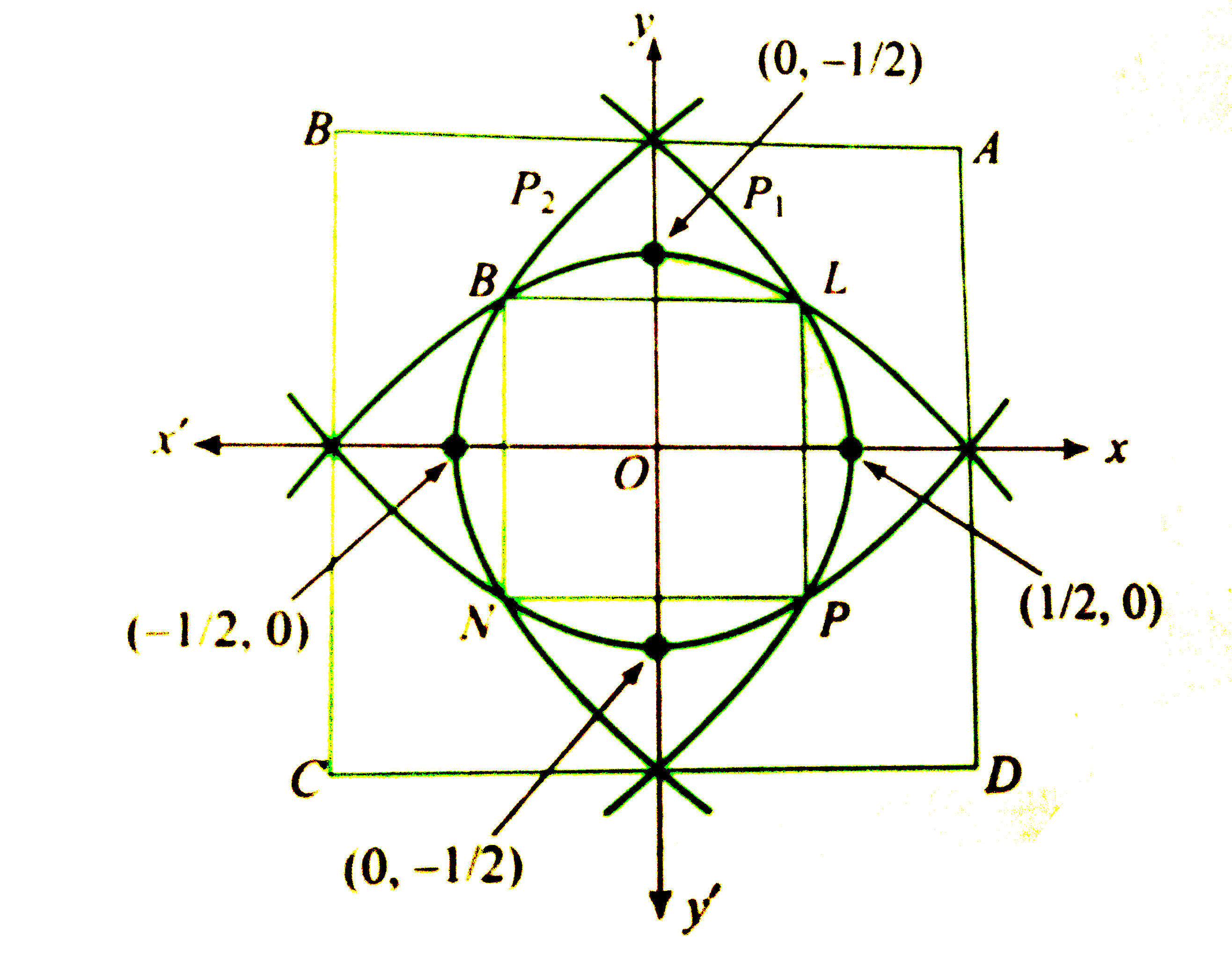
Consider a square with vertices at (1,1),(−1,1),(−1,−1)and(1,−1). Let S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area. Solution in Tamil

Let us consider any point (x,y) inside the square such that its distance from origin is less than its distance from any of the edges. Consider edge AD. Therefore,
OP<PM
⇒ √(x2+y2)<1−xory2<−2(x−12) (1)
Above represents all points within the parabola y2=1−2x.
If we consider the edge BC, then OP<PN will imply
y2<2(x+12) (2)
Similarly, if we consider the edges AB and CD, we will have
x2<−2(y−12) (3)
x2<2(y+12) (4)
Hence, S consists of the region bounded by four parabolas meeting
the axes at (±12,0)and(0,±12)
The point L is intersection of P1andP3 given by (1) and (3).
Solving, we get
y2−x2=−2(x−y)=2(y−x)
or y−x=0
or y=x
⇒ x2+2x−1=0
or (x+1)2=2
or x=√2−1 as x is + ve
∴ L is (√2−1,√2−1).
∴ Total area = 4[Square of side (√2−1)+2∫1/2√2−1√1−√2xdx]
=4{(√2−1)2+2∫1/2√2−1√(1−2x)dx}
=4[3−2√2−23{(1−2x)3/2}1/2√2−1]
=4[3−2√2−23{0−(1−2√2+2)3/2}]
=4[3−2√2+23(3−2√2)3/2]
=4(3−2√2)[1+23√(3−2√2)]
=4(3−2√2)[1+23(√2−1)]
=43(3−2√2)(1+2√2)=43[(4√2−5)]
=16√2−203 sq. units.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.19videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.214videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
05:34View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
06:40View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
07:22View SolutionLet S = {(x,y): (y(3x-1))/(x(3x-2))<0}, S'= {(x,y) in AxxB: -1 leqAleq1, -1 leqBleq1}, then the area of the region enclosed by all points in SnnS' is
08:45View SolutionHECTARES: The area of a region formed by a square of side 1 hectometer (1 hm) is called a hectare written as 1hm2. Square Kilometer: The area of a region formed by a square of side 1 km is called a square kilometer written as 1 km^2 .
03:34View SolutionConsider two regions
R1:points P are nearer to (1,0) than to x=−1.
R2:Points P are nearer to (0,0) than to (8,0) Find the area of the region common to R1andR2.03:11View SolutionConsider the region S of complex numbers a such that ∣∣z2−az+1∣∣=1, where |z|=1 . Then area of S in the Argand plane is
23:23View SolutionConsider a square with vertices at (1,1)(−1,1)(−1,−1)and(1,−1). Let S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.
07:58View Solutionमाना वर्ग के शीर्ष (1,1),(−1,1),(−1,−1) तथा (1,−1) है | माना वर्ग के अन्दर के सभी बिन्दुओ मूल बिन्दु से किसी भी भुजा कि अपेक्षा पास हो, का क्षेत्र S है | S को क्षेत्र बनाइए तथा इसका क्षेत्रफल ज्ञात कीजिए |
04:43View SolutionFind the area of the square formed by the points (0, -1), (2, 1) (0, 3) and (-2, 1) as vertices.
03:29View SolutionConsider a square with vertices at (1,1)(−1,1)(−1,−1)and(1,−1). Let S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.
05:28View SolutionConsider a square with vertices at (1,1),(−1,1),(−1,−1),and(1,−1). Set S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.
03:34View SolutionConsider a square with vertices at (1,1),(−1,1),(−1,−1),and(1,−1). Set S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.
05:32View SolutionConsider two regions
R1:points P are nearer to (1,0) than to x=−1.
R2:Points P are nearer to (0,0) than to (8,0) Find the area of the region common to R1andR2.06:15View SolutionConsider the region S of complex numbers a such that ∣∣z2−az+1∣∣=1, where |z|=1 . Then area of S in the Argand plane is
20:10View Solution

