The equation of the diagonals of a rectangle are y+8x−17=0 and y−8x+7=0. If the area of the rectangle is 8squnits then find the sides of the rectangle
x=1
x+y=1
y=9
x−2y=3
The correct Answer is:A, C
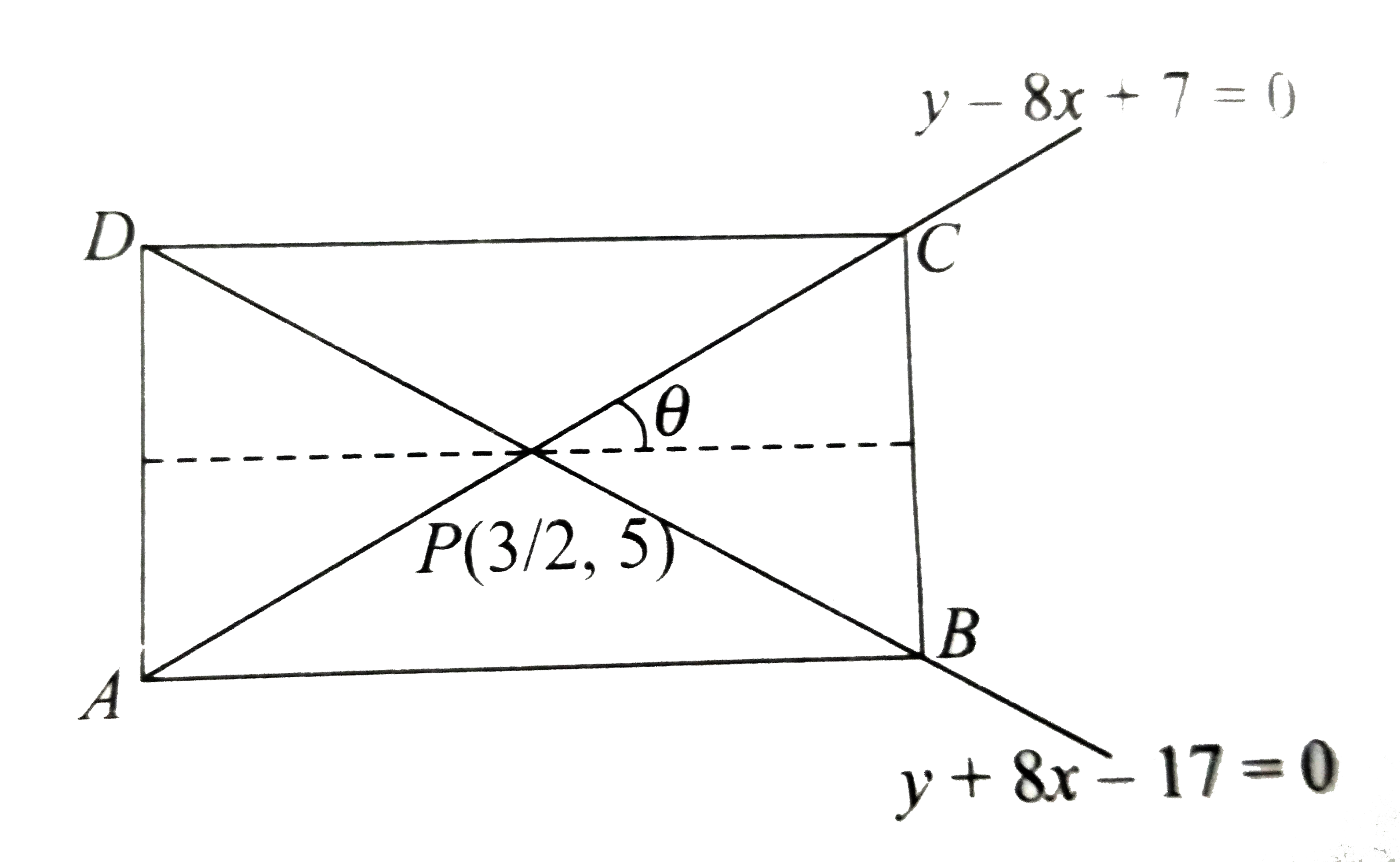
The intersection point of the given diagonals is P≡(32,5)
Equation of angle bisectors of the diagonals are
y+8x−17√65=±y−8x+7√65
or x=32 and y=5
Let the length of BC be a and that of CD be b.
Then tan=a/2b/2=ab=8.
Also ab=8
⇒a=8,b=1.
So equations of side are y=1,y=9,x=1 and x=2
Topper's Solved these Questions
Similar Questions
The equation of the diagonals of a rectangle are y+8x−17=0 and y−8x+7=0. If the area of the rectangle is 8squnits then find the sides of the rectangle
View SolutionThe length of a rectangle exceeds its width by 8 cm and the area of the rectangle is 240 sq. cm. Find the dimensions of the rectangle.
View SolutionThe length of a rectangle exceeds its width by 8 cm and the area of the rectangle is 240 sq. cm. Find the dimensions of the rectangle.
View Solutionfind the length of the diagonal of a rectangle whose sides are 8 m and 6m.
View Solutionfind the length of the diagonal of a rectangle whose sides are 8 m and 6m.
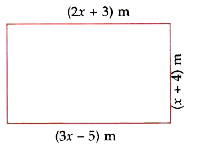
View SolutionThe measurements of the sides of a rectangle are given. Find
(i) the value of x.
(ii) the area of the rectangle
(iii) the perimeter of the rectangle .
View SolutionFind the equations of the diagonals of a rectangle whose sides are x + 1 = 0, x - 4 = 0, y + 1 = 0 and y - 2 = 0.
View SolutionWhat is the area of the rectangle whose diagonal is 17 cm and breadth is 8 cm?
View SolutionWhat is the area of the rectangle whose diagonal is 17 cm and breadth is 8 cm?
View SolutionThe equation of one side of a rectangle is 3x−4y−10=0 and the coordinates of two of its vertices are (−2,1)and(2,4). Then, the area of the rectangle is
View Solution
