In a ΔABC,A=(2,3) and medians through B and C have equations x+y−1=0 and 2y−1=0
Equation of median through A is Solution in Tamil
x+y=4
5x−3y=1
5x+3y=1
5x=3y
The correct Answer is:B
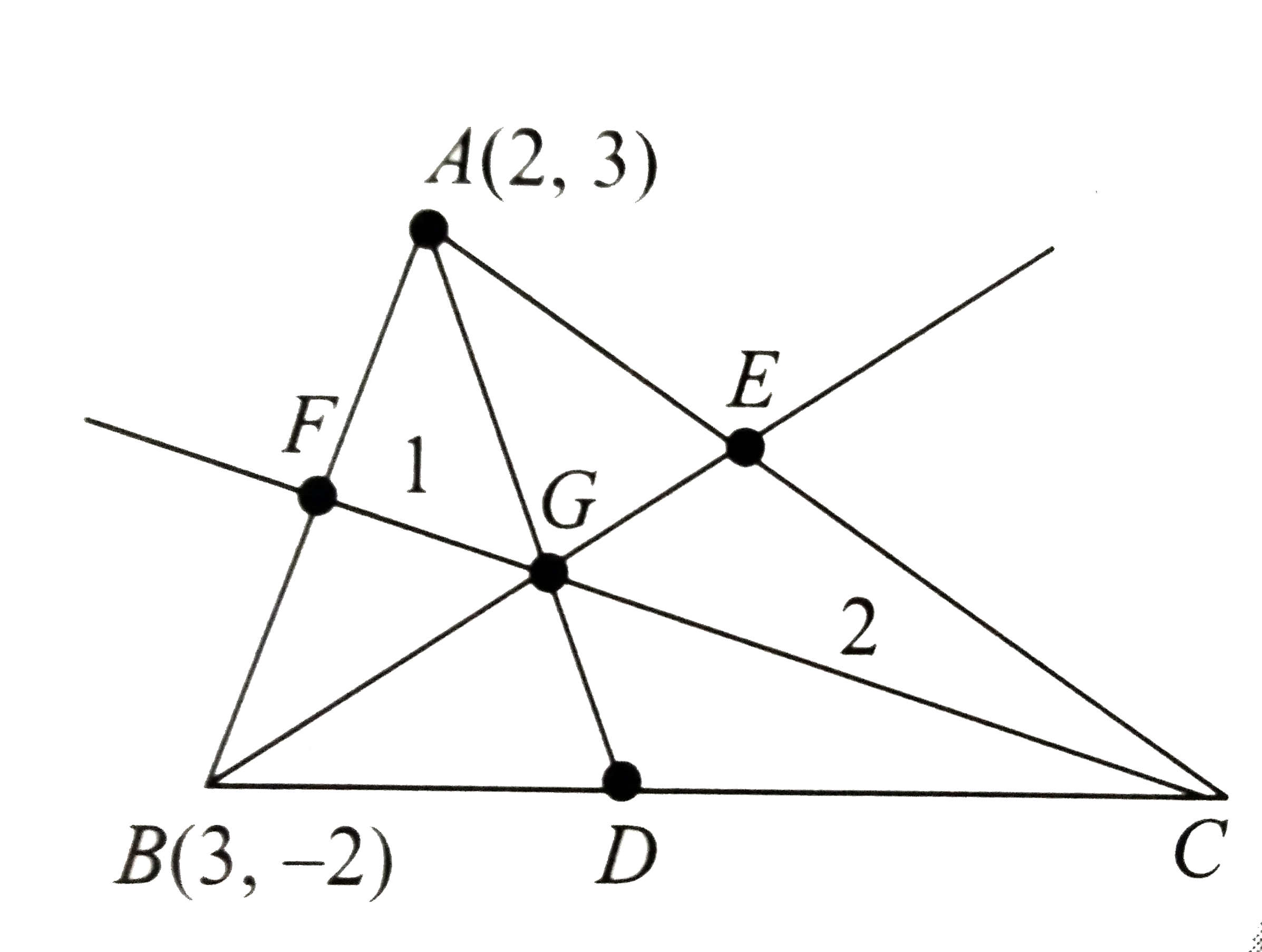
Centroid is the point of intersection of x+y−1=0,2y−1=0 or D(12,12)
Slope of AD is 3−122−12=53
∴ Equation of AD is y−3=53(x−2) or 5x−3y−1=0
A point of CF:2y−1=0 is (α,12)
Let this be the midpoint of AB.
∴ B is (2α−2,−2) which lies on median BE:x+y−1=0
∴2α−2−2−1=0∴α=52
∴B(3,−2)
G divides CF in 2:1
∴C=(−72,12)
∴ Equation of BC is y+212+2=x−3−72−3
or y+25=x−3−13
or 5x+13y+11=0
Topper's Solved these Questions
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- STATISTICSBOOK - CENGAGECHAPTER - STATISTICSEXERCISE - JEE Previous Year
10 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year
4 Videos
Similar Questions
The point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionIf the mean deviation of number 1,1+d, 1+2d,…., 1+100d from their mean is 255, then d is equal to
View Solutionabout to only mathematics
View SolutionFind the equation of the sides of a triangle ABC with A(1,3) as a vertex and x-2y+1=0 and y-1=0 as the equation of two of its medians.
View SolutionThe vertices of ΔABC are A(−3,2), B(0,3) and C(1,0). Find the equation of the median through B.
View SolutionIn a ΔABC,A=(2,3) and medians through B and C have equations x+y−1=0 and 2y−1=0
Equation of median through A is
View SolutionIn a ΔABC,A=(2,3) and medians through B and C have equations x+y−1=0 and 2y−1=0
Equation of side BC is
View SolutionΔABC के शीर्ष A(−3,2),B(0,3) और C(1,0) है। B से होकर जाने वाली रेखा माध्यिका का समीकरण ज्ञात कीजिए ।
View SolutionA(0 , - 1) , B(2 , 1) and C(0 , 3) are the vertices of ΔABC then median through B has a length .......units.
View SolutionIn a triangle ABC, coordinate of A are (1,2) and the equations of the medians through B and C are respectively, x+y=5&x=4. Then area of ΔABC (in sq. units) is:
View SolutionFind the length of the perpendicular from the vertex B of ΔABC to the median through C if A is (−10,−13), B is (−2,3) and C is (2,1).
View SolutionIn a ΔABC,A=(2,3) and medians through B and C have equations x+y−1=0 and 2y−1=0
Equation of median through A is
View SolutionIn a ΔABC,A=(2,3) and medians through B and C have equations x+y−1=0 and 2y−1=0
Equation of side BC is (a) 5x+13y+11=0 (b) 5x−3y=1 (c) 5x=3y (d) 5x+13y−11=0
View SolutionGiven the vertices A(10, 4), B(-4, 9) and C(-2, -1) of ΔABC, find
the equation of the median through A
View Solution
