Triangle ABC is right angled at A. The circle with centre A and radius AB cuts BC and AC internally at D and E respectively. If BD=20 and DC=16 then the length AC equals (A) 6sqrt21 (B) 6sqrt26 (C) 30 (D)32
30
32
The correct Answer is:B
(1)
Also,
(2)
From (1) and (2)
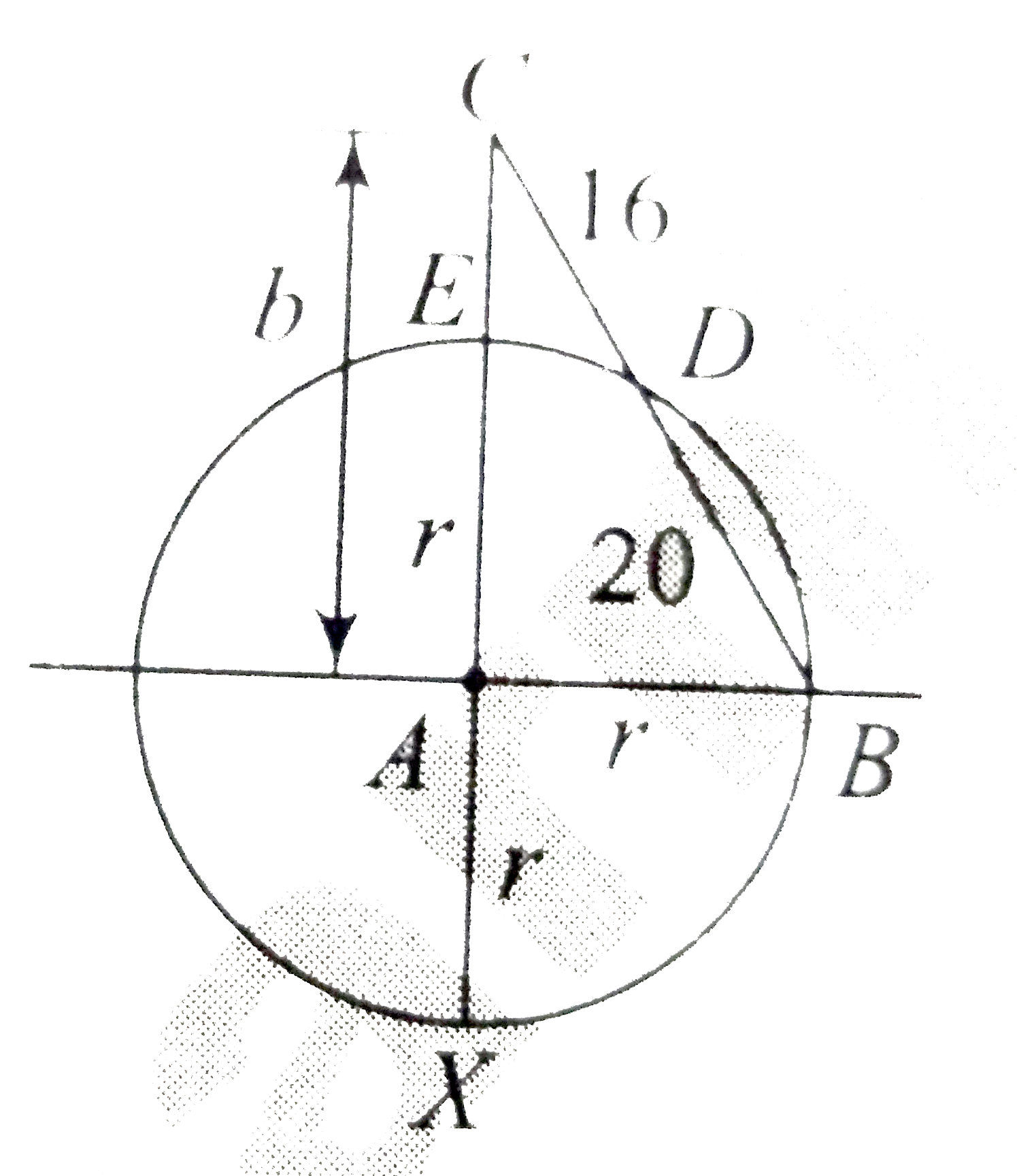
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Multiple Correct Answers Type9videos
CIRCLES
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE6videos
CIRCLE
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - JEE Advanced Previous Year14videos
COMPLEX NUMBERS
Similar Questions
The angle A of the triangle ABC is a right angle. The circle on AC as diameter cuts BC at point D. If BD=9cm and DC = 7 cm, calculate the length of AB.
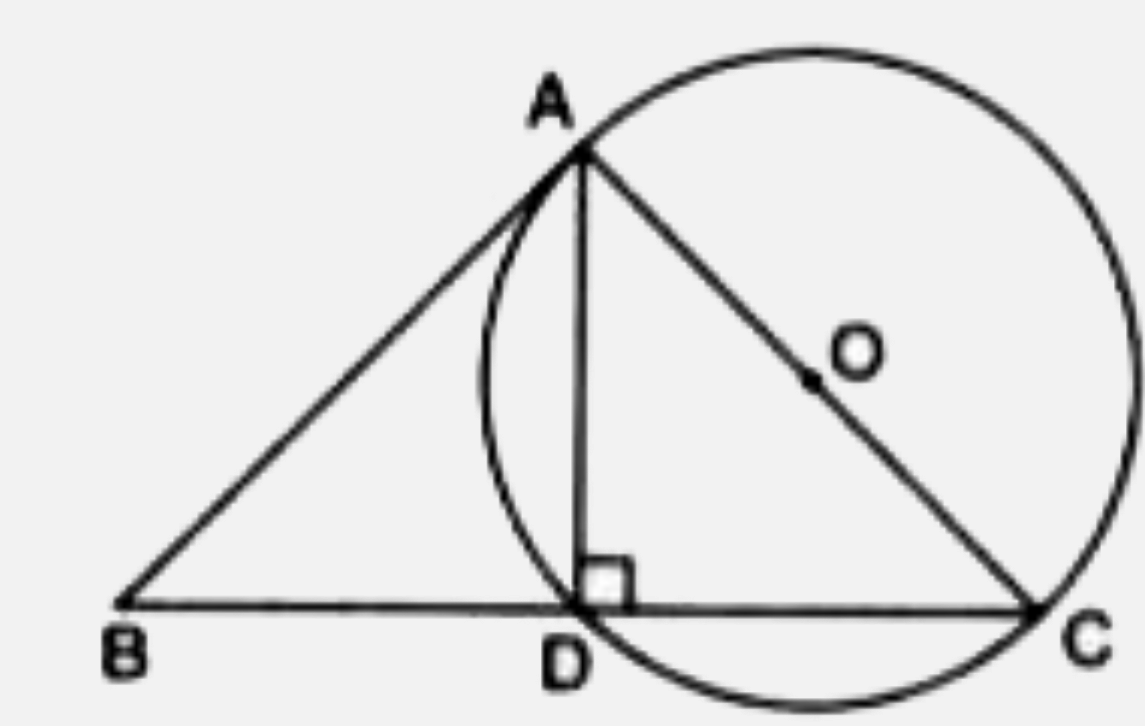 View Solution
View SolutionABC is right angle triangle , (right angled at B ) incircle touches the sides AB, BC & AC at F, E, & D respectively . If BD is prependicular to AC then , find the ratio of AF to FB .
View Solution
Knowledge Check
- Question 1 - Select One
Triangle ABC inscribes a circle with centre O and inradius √6cm. The inradius OD divides side BC at D, such that BD=2 cm and DC=8 cm. Find the ratio AB:AC.
A4:7B5:7C4:5Dcannot be determined - Question 2 - Select One
In triangle ABC , sides AB and AC are extended to D and E, respectively, such that AB=BD and AC =CE,F∈dDE,ifBC=6 cm.
A3 cmB6cmC9 cmD12 cm - Question 3 - Select One
ΔABC has a right angle at A. If BC=√2andAB=AC=1 then sinB is equal to
(a) 1√2
(b) √2
(c) √32
(d) √3A1√2B√2C√32D√3
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively . Prove that BD = DC.
 View Solution
View SolutionABC is right angled at B .On the side AC a point D is taken such that AD=DC and AB=BD. Find the measure of ∠CAB
View SolutionIf ΔABC is right - angle at B, AB = 6 units ∠=30∘ then AC is equal to
View SolutionΔABC is a right angle triangle and ∠ABC=90∘. If the length of AB and BC is 12 cm and 16 cm respectively, then find the length of BD. (Where, BD⊥AC)
View SolutionΔABC has a right angle at A. If BC = √2andAB=AC=1, then sin B is equal to
View Solution

