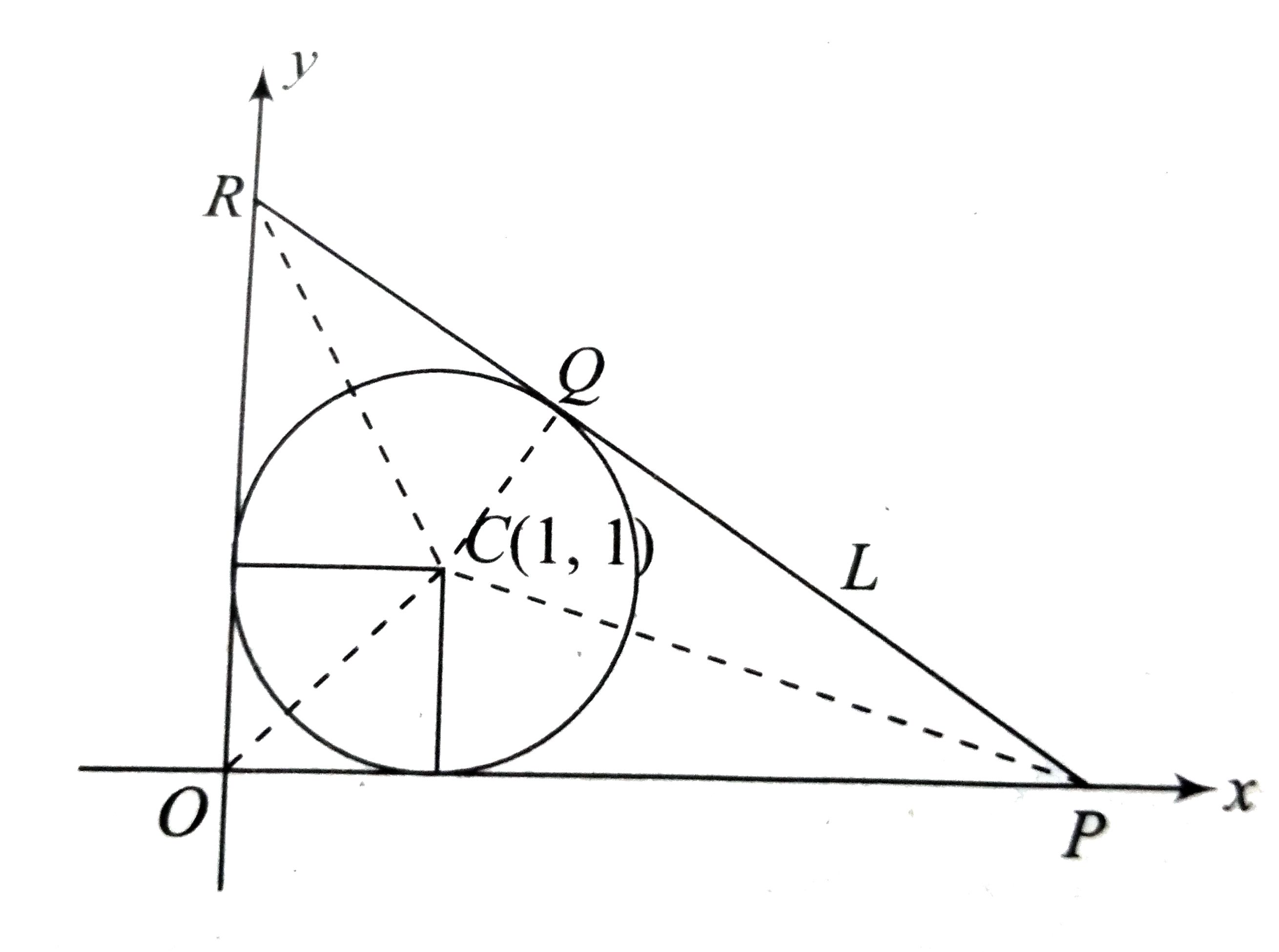
In the diagram as shown, a circle is drawn with centre $C (1, 1)$ and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals $θ$ where $0 < θ < \frac{π}{2}$ .
Equation of the line PR is

A

$x cos θ + y sin θ = sin θ + cos θ + 1$

B

$x sin θ + y cos θ = cos θ + sin θ - 1$

C

$x sin θ + y cos θ = cos θ + sin θ + 1$

D

$x tan θ + y = 1 + cot (\frac{θ}{2})$

Text Solution

Verified by Experts

The correct Answer is:C

$m_{C Q} = cot θ$
$m_{P R} = - tan θ$
Equation of PR is
$y - (1 + cos θ) = - tan θ (x - (1 + sin θ))$
or $y + x θ = (1 + cos θ) + tan θ (1 + sin θ)$
$= \frac{cos θ (1 + cos θ) + sin θ (1 + sin θ)}{cos θ}$
or $y + x tan θ = \frac{1 + cos θ + sin θ}{cos θ}$
or $x sin θ + y cos θ = (cos θ + sin θ + 1)$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One

In the diagram as shown, a circle is drawn with centre $C (1, 1)$ and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals $θ$ where $0 < θ < \frac{π}{2}$ .
Area of triangle OPR when $θ = π / 4$ is
A $(3 - 2 \sqrt{2})$
B $(3 + 2 \sqrt{2})$
C $(6 + 4 \sqrt{2})$
Dnone of these
Question 2 - Select One
A tangent to the hyperbola meets x-axis at P and y-axis at Q. Lines PR and QR are drawn such that OPRQ is a rectangle (where O is the origin) then R lies on
A $\frac{4}{x^{2}} + \frac{2}{y^{2}} = 1$
B $\frac{2}{x^{2}} - \frac{4}{y^{2}} = 1$
C $\frac{2}{x^{2}} + \frac{4}{y^{2}} = 1$
D $\frac{4}{x^{2}} - \frac{2}{y^{2}} = 1$
Question 3 - Select One
a tangent to the hyperbole $\frac{X^{2}}{4} - \frac{y^{2}}{2} = 1$ meets x-axis at P and y-axis at Q. Lines PR and QR are deawn such that OPRQ is a rectangle (where O is the origin). Then R lies on :
A $\frac{4}{x^{2}} + \frac{2}{y^{2}} = 1$
B $\frac{2}{x^{2}} - \frac{4}{y^{2}} = 1$
C $\frac{2}{x^{2}} + \frac{4}{y^{2}} = 1$
D $\frac{4}{x^{2}} - \frac{2}{y^{2}} = 1$

CENGAGE-CIRCLES-Comprehension Type

Home
Ask Doubt
Profile