Two circles are drawn through the points $(a, 5 a) and (4 a, a)$ to touch the y-axis. Prove that they intersect at angle ${tan}^{- 1} (\frac{40}{9}) .$

A

${tan}^{- 1} (4 / 3)$

B

${tan}^{- 1} (40 / 9)$

C

${tan}^{- 1} (84 / 187)$

D

$π / 4$

Text Solution

Verified by Experts

The correct Answer is:B

Equation of any circle through the given points is:
$(x - a) (x - 4 a) + (y - 5 a) (y - a) + λ (4 x + 3 y - 19 a) = 0$ , for some $λ \in R$ .
As it touches the y-axis, putting $x = 0$ and comparing discriminant of resulting quadratic equation in x to 0, we get
$∴ {(- 3 a + \frac{3 λ}{2})}^{2} = 9 a^{2} - 19 λ a$
$∴ λ = 0, \frac{- 40 a}{9}$ .
$∴$ The required circles are
$x^{2} + y^{2} - 5 a x - 6 a y + 9 a^{2} = 0$
$x^{2} + y^{2} - 5 a x - 6 a y + 9 a^{2} - \frac{40 a}{9} (4 x + 3 y - 19 a) = 0$
Hence centres are $(\frac{5 a}{2}, 3 a)$ and $(\frac{205 a}{18}, \frac{29 a}{3})$

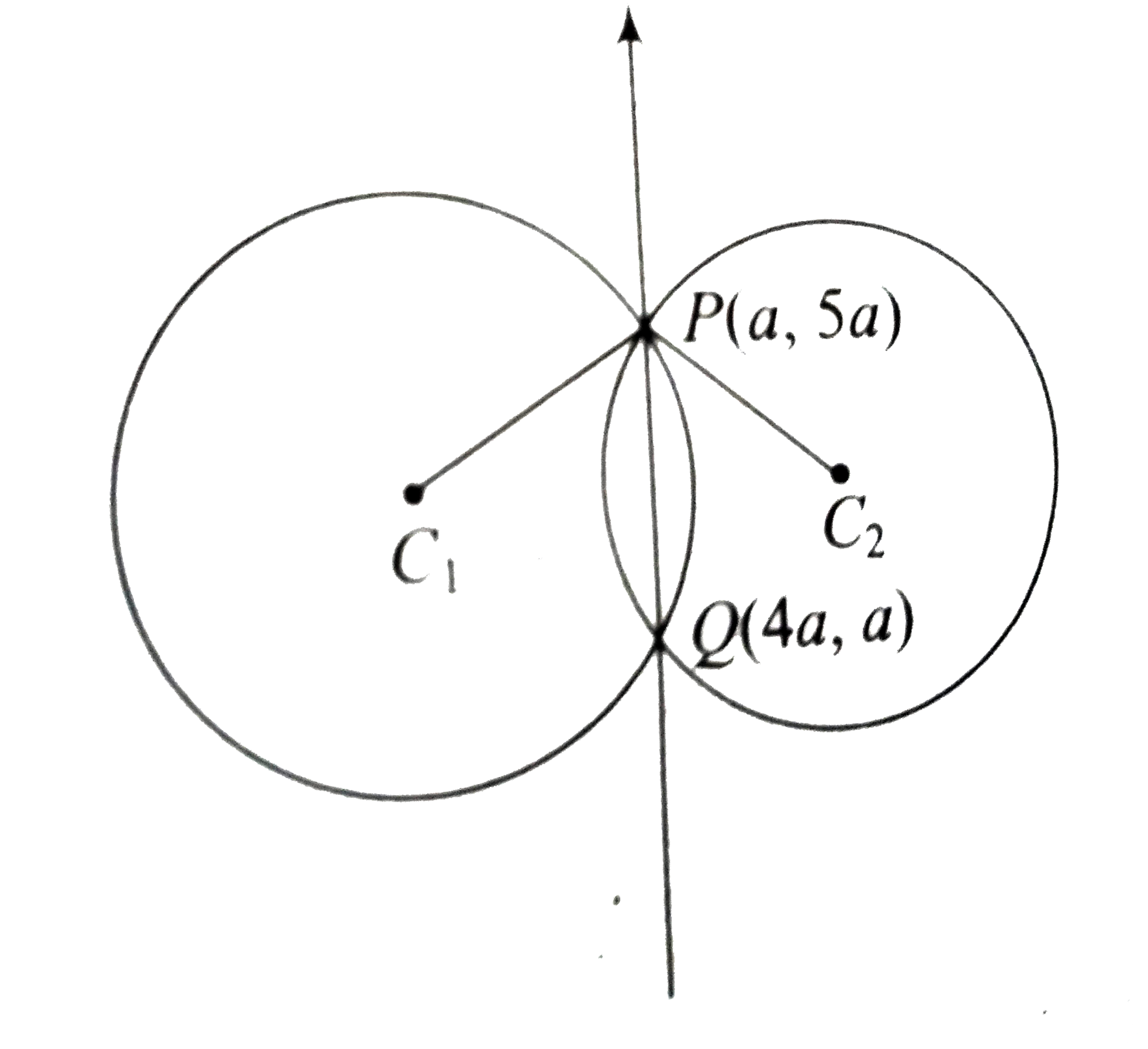
The centres of the given circles are:
$C_{1} (\frac{205 a}{18}, \frac{29 a}{3})$ and $C_{2} (\frac{5 a}{2}, 3 a)$
Now, the angle of intersection $θ$ of these two circles is the angle between the radius vectors a the common point P to the two circles.
i.e., $∠ C_{1} P C_{2} = θ$
and slope of $C_{2} P = \frac{5 a - 3 a}{a - \frac{5 a}{2}} = - \frac{4}{3}$
So, $tan θ = \frac{\frac{84}{187} + \frac{4}{3}}{1 - \frac{84}{187} \times \frac{4}{3}} = \frac{252 + 748}{561 - 336} = \frac{40}{9}$
$\Rightarrow θ = {tan}^{- 1} (\frac{40}{9})$

Updated on:21/07/2023

|

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Equation of circle passing through the points (4, 3) and (2,5) and touching the axis of y is
A $x^{2} + y^{2} - 20 x - 22 y + 121 = 0$
B $x^{2} + y^{2} - 4 x - 6 y + 9 = 0$
C $x^{2} + y^{2} - 10 x - 6 y + 13 = 0$
D $x^{2} + y^{2} + 4 x + 6 y + 9 = 0$
The circles which can be drawn to pass through (3,0) and (5,0) and to touch the y-axis intersect at an angle $θ$ , then $cos θ$ is equal to
A $7 / 8$
B $1 / 2$
C0
Dnone of these

CENGAGE-CIRCLES-Comprehension Type

Home
Ask Doubt
Profile