Tangents drawn from point of intersection A of circles x2+y2=4and(x−√3)2+(y−3)2=4 cut the line joinihg their centres at B and C Then triangle BAC is
equilateral triangle
right angle triangle
obtuse angle triangle
isosceles triangle and ∠ABC=π6
The correct Answer is:A
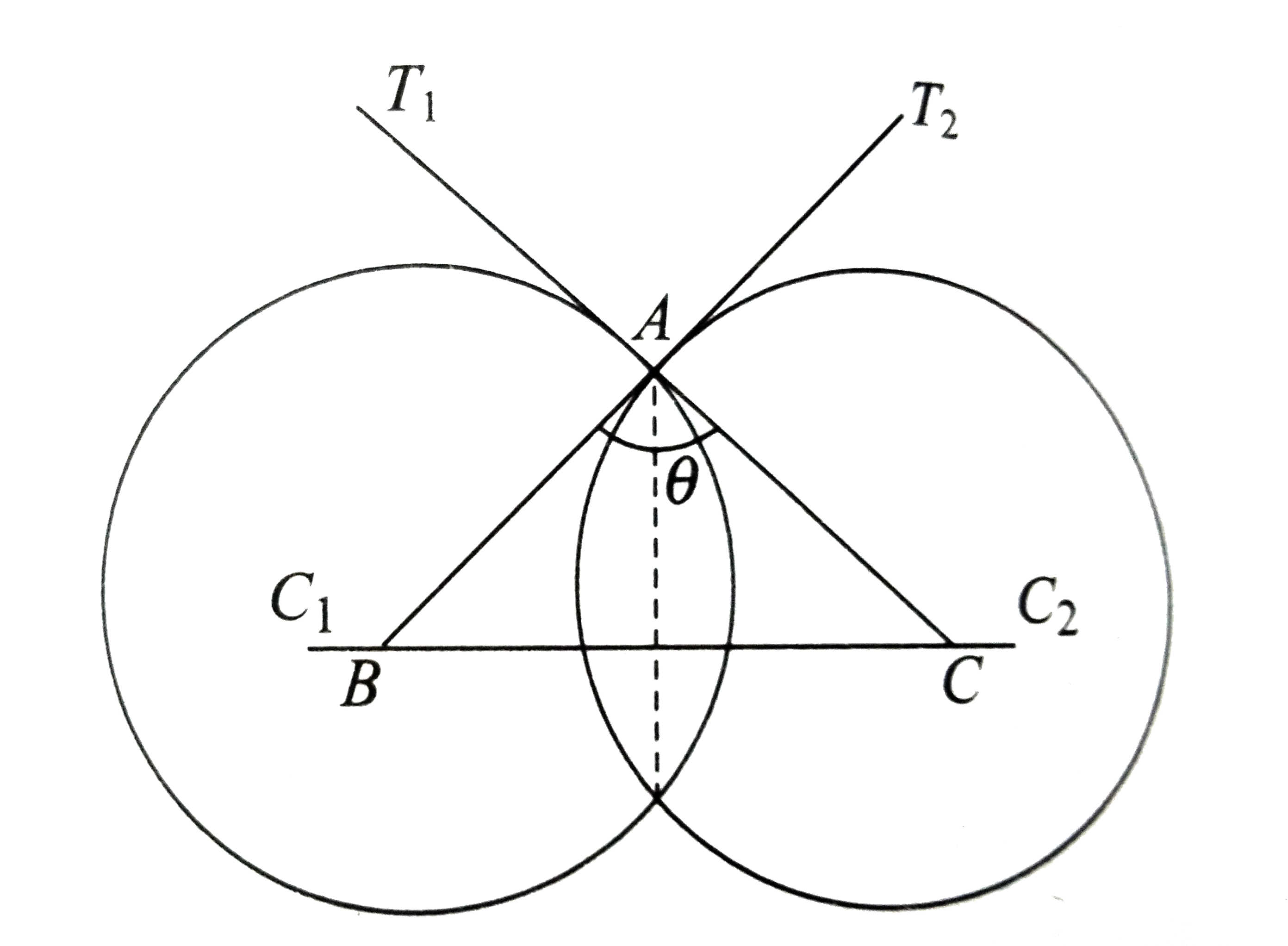
Radii of the circles are same
⇒AB=AC
Also, if θ is the angle between the tangents, then
cosθ=12−4−42(2)(2)=12
⇒θ=π3
Hence, ΔABC is an equilateral triangle.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Multiple Correct Answers Type9videos
CIRCLES
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE6videos
CIRCLE
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - JEE Advanced Previous Year14videos
COMPLEX NUMBERS
Similar Questions
Tangents drawn from point of intersection A of circles x2+y2=4and(x−√3)2+(y−3)2=4 cut the line joinihg their centres at B and C Then triangle BAC is
View SolutionTangents drawn from point of intersection A of circles x2+y2=4and(x−√3)2+(y−3)2=4 cut the line joinihg their centres at B and C Then triangle BAC is
View Solution
Knowledge Check
- Question 1 - Select One
Tangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B the equation of the circumcircle of △PAB is
Ax2+y2÷4x−6y+19=0Bx2+y2−4x−10y+19=0Cx2+y2−2x+6y−29=0Dx2+y2−6x−4y+19=0 - Question 2 - Select One
Tangents drawn from the point (4, 3) to the circle x2+y2−2x−4y=0 are inclined at an angle
Aπ/6Bπ/4Cπ/3Dπ/2 - Question 3 - Select One
Tangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
Ax2+y2+4x−6y+19=0Bx2+y2−4x−10y+19=0Cx2+y2−2x+6y−20Dx2+y2−6x−4y+19=0
Tangents drawn from the point (4, 3) to the circle x2+y2−2x−4y=0 are inclined at an angle
View SolutionTangents are drawn from the point (4,3) to circle x2+y2=9. The area of the triangle forme by them and the line joining their point of contact is
View SolutionIf tangents be drawn to the circle x2+y2=12 at its points of intersection with the circle x2+y2−5x+3y−2=0, then the tangents intersect at the point
View SolutionA straight line is drawn through the centre of the circle x2+y2−2ax=0 line x+2y=0 parallel to the straight and intersecting the circle at A and B. Then the area of triangle AOB is
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View Solution

