Two circle touch the x-axes and the line $y = m x$ they meet at (9,6) na d at one more point and the product of their radus is $\frac{117}{2}$ then the value of m is

A

$2 \sqrt{2}$

B

$\sqrt{2}$

C

$\frac{1}{\sqrt{2}}$

D

none of these

Text Solution

Verified by Experts

The correct Answer is:A

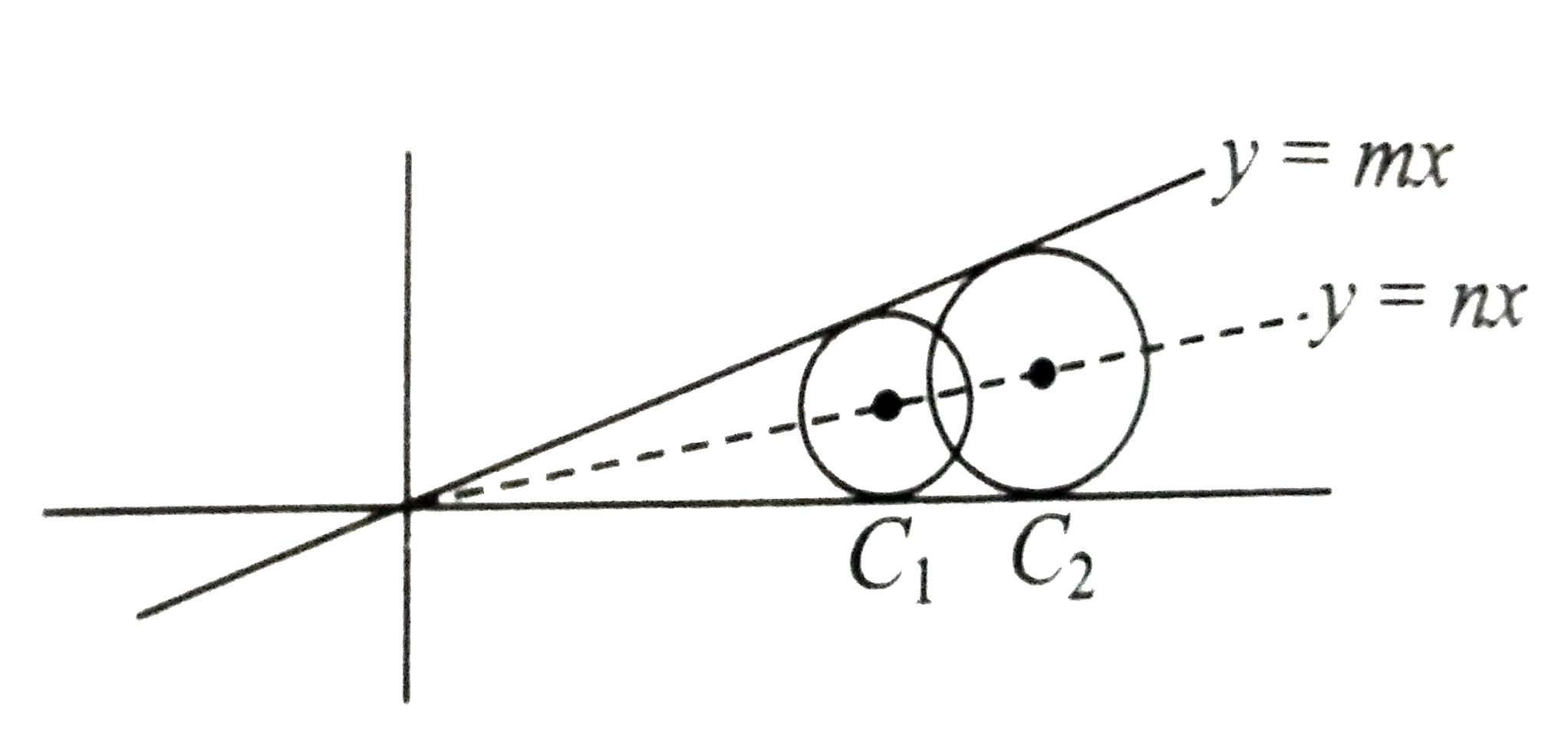
Let the centre of $C_{1}$ be (a,na)
$\Rightarrow {(a - 9)}^{2} + {(n a - 6)}^{2} = {(n a)}^{2}$ (1)
Also, $m = \frac{2 n}{1 - n^{2}}$
From (1), $a^{2} + 117 - 18 a - 12 n a = 0$
$\Rightarrow a^{2} - a (18 + 12 n) + 117 = 0$
$\Rightarrow a_{1} a_{2} = 117$
$\Rightarrow r_{1} r_{2} = n^{2} a_{1} a \times 117 = \frac{117}{2}$
$\Rightarrow n^{2} = \frac{1}{2} ∴ m = 2 \sqrt{2}$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If the line $y = m x$ , meets the lines $x + 2 y = 1$ and $2 x - y + 3 = 0$ at one point only then $m = ?$
A $1$
B $- 1$
C $- 2$
DNone of these
Question 2 - Select One
If the line $y = m x$ meets the lines $x + 2 y - 1 = 0$ and $2 x - y + 3 = 0$ at the same point, then m is equal to
A1
B $- 1$
C2
D $- 2$

CENGAGE-CIRCLES-Question Bank

Home
Ask Doubt
Profile