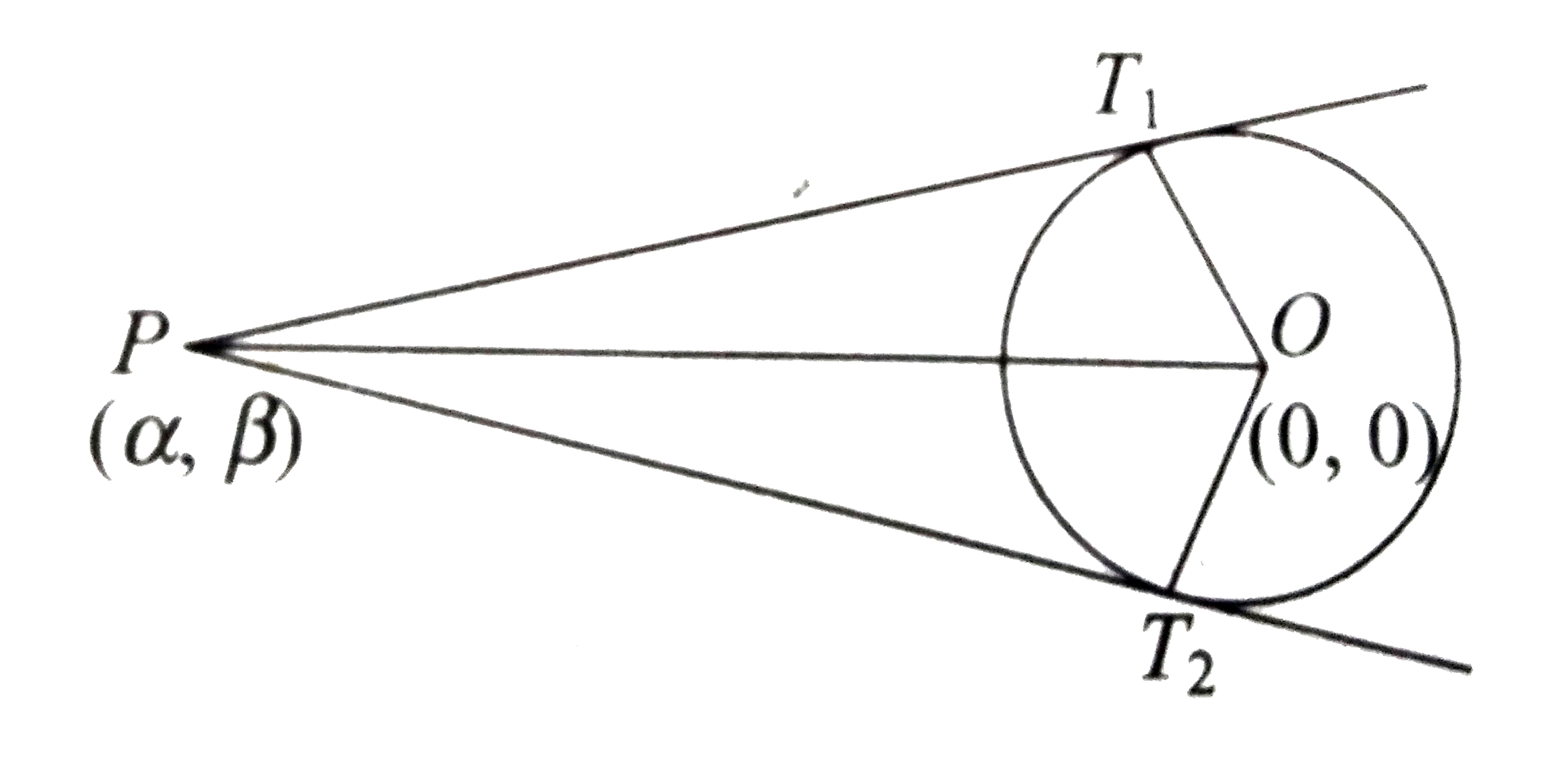
Tangents $P T_{1}, and P T_{2}$ , are drawn from a point P to the circle $x^{2} + y^{2} = a^{2}$ . If the point P line $P x + q y + r = 0$ , then the locus of the centre of circumcircle of the triangle $P T_{1} T_{2}$ is

A

$p x + q y = r$

B

${(x - p)}^{2} + {(y - q)}^{2} = r^{2}$

C

$p x + q y = \frac{r}{2}$

D

$2 p x + 2 q y + r = 0$

Text Solution

Verified by Experts

The correct Answer is:D

$P, T_{2}, Q, T_{1}$ are concylic points with PO as diameter.
Thus, the circumcentre of $Δ P T_{1} T_{2}$ is $(\frac{α}{2}, \frac{β}{2})$ .
New $(α, β)$ lies on $p x + q y + r = 0$
i.e, locus of $(\frac{α}{2}, \frac{β}{2})$ is $2 p x + 2 q y + r = 0$ .

|

Updated on:21/07/2023

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Tangents drawn from the point P(1,8) to the circle $x^{2} + y^{2} - 6 x - 4 y - 11 = 0$ touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
A $x^{2} + y^{2} + 4 x - 6 y + 19 = 0$
B $x^{2} + y^{2} - 4 x - 10 y + 19 = 0$
C $x^{2} + y^{2} - 2 x + 6 y - 20$
D $x^{2} + y^{2} - 6 x - 4 y + 19 = 0$
Question 2 - Select One
A pair of tangents are drawn from a point P to the circle $x^{2} + y^{2} = 1$ . If the tangents make an intercept of 2 on the line x=1, the locus of P is
Astraight line
Bpair of lines
Ccircle
Dparabola
Question 3 - Select One
Tangents drawn from the point P(1,8) to the circle $x^{2} + y^{2} - 6 x - 4 y - 11 = 0$ touch the circle at the points A and B the equation of the circumcircle of $△ P A B$ is
A $x^{2} + y^{2} \div 4 x - 6 y + 19 = 0$
B $x^{2} + y^{2} - 4 x - 10 y + 19 = 0$
C $x^{2} + y^{2} - 2 x + 6 y - 29 = 0$
D $x^{2} + y^{2} - 6 x - 4 y + 19 = 0$

CENGAGE-CIRCLES-Question Bank

Home
Ask Doubt
Profile