x2+y2=16andx2+y2=36 are two circles. If PandQ move respectively on these circles such that PQ=4 then the locus of mid-point of PQ is a circle of radius Solution in Tamil
√20
√22
√30
√32
The correct Answer is:B
Using Apollonius theorem in ΔPCQ, we get
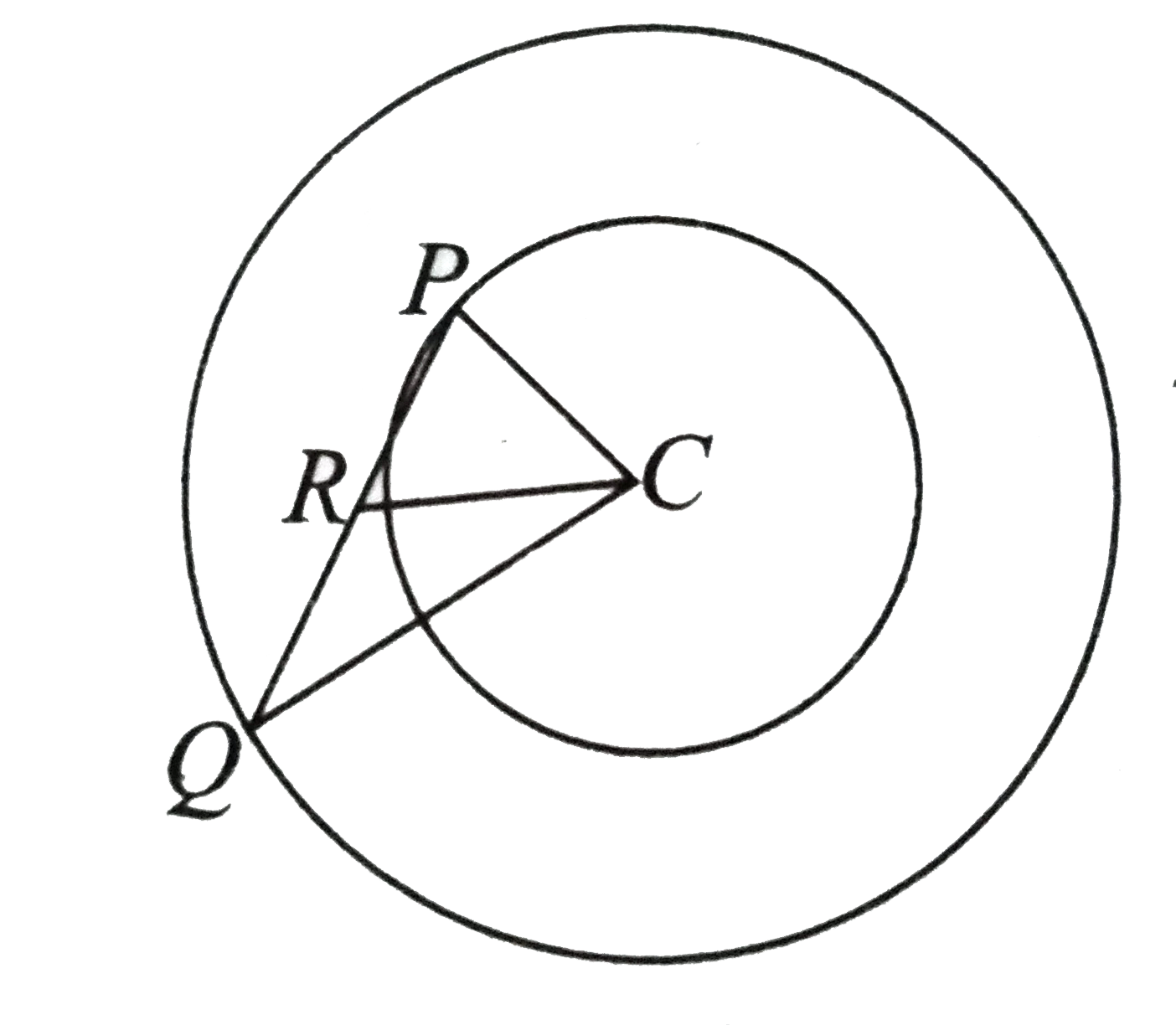
CP2+CQ2=2(CR2+RQ2)
⇒16+36=2(CR2+(42)2)
⇒52=2(CR2+4)
⇒CR=√22
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Multiple Correct Answers Type9videos
CIRCLES
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE6videos
CIRCLE
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - JEE Advanced Previous Year14videos
COMPLEX NUMBERS
Similar Questions
The line 3x+6y=k intersects the curve 2x2+3y2=1 at points AandB . The circle on AB as diameter passes through the origin. Then the value of k2 is__________
04:52View SolutionIn the diagram as shown, a circle is drawn with centre C(1, 1) and radius I and a line L. The line Lis tangential to the circle at Q. Further L meet the y-axis at R and the x-axis at Pis such a way that the angle OPQ equals θ where 0<θ<π2 The coordinates of Q are
02:29View SolutionFind the derivative of y=ln(cosx2).
09:30View SolutionLet z=x+iy be a complex number where xandy are integers. Then, the area of the rectangle whose vertices are the roots of the equation zz3+zz3=350 is 48 (b) 32 (c) 40 (d) 80
03:17View Solutionx^(2)+y^(2)=16 and x^(2)+y^(2)=36 are two circles.If P and Q move respectively on these circles such that PQ=4 then the locus of mid-point of PQ is a circle of radius
07:27View Solutionif P is a variable point and PQ and PRare the tangent drawn to the circle x^(2)+y^(2)=9. Let QR be always touching the circle x^(+)y^(2)=4 then locus of P is
05:27View SolutionThe circles x^(2)+y^(2)+2ax-c^(2)=0 and x^(2)+y^(2)+2bx-c^(2)=0 intersect at A and B A line through A meets one circle at P and B parallel line through B meets the other circle at Q.Show that the locus of the mid-point of PQ is a circle.
04:17View SolutionIf P is a point on the hyperbola (x^(2))/(16)-(y^(2))/(9)=1 and Q be the focus of the parabola y^(2)=8x then locus of mid-point of PQ is
06:32View SolutionIf a tangent to the circle x2+y2=1 intersects the coordinate axes at distinct points P and Q, then the locus of the mid-point of PQ is :
03:50View SolutionIf a tangent to the circle x2+y2=1 intersects the coordinate axes at distinct point P and Q. then the locus of the mid- point of PQ is
View SolutionIF (α,β) is a point on the chord PQ of the circle x2+y2=25, where the coordinates of P and Q are (3, -4) and (4, 3) respectively, then
05:33View SolutionThe line x =2 y intersects the ellipse x24+y2=1 at the points P and Q . The equation of the circle with pq as diameter is _
02:41View SolutionA tangent to the circle x2+y2=4 meets the coordinate axes at P and Q. The locus of midpoint of PQ is
08:15View SolutionIf the polar of a point on the circle x2+y2=p2 with respect to the circle x2+y2=q2 touches the circle x2+y2=r2 then p,q r are in
04:58View Solutionx2+y2=16andx2+y2=36 are two circles. If PandQ move respectively on these circles such that PQ=4 then the locus of mid-point of PQ is a circle of radius
06:41View Solution

