A variable line moves in such a way that the product of the perpendiculars from (4, 0) and (0, 0) is equal to 9. The locus of the feet of the perpendicular from (0, 0) upon the variable line is a circle, the square of whose radius is Solution in Tamil
13
15
19
23
The correct Answer is:A
Let the foot of the perpendicular from origin upon the variable line be (x1,y1).
So, equation of the variable line is:
×1+yy1−(x21+y21)=0
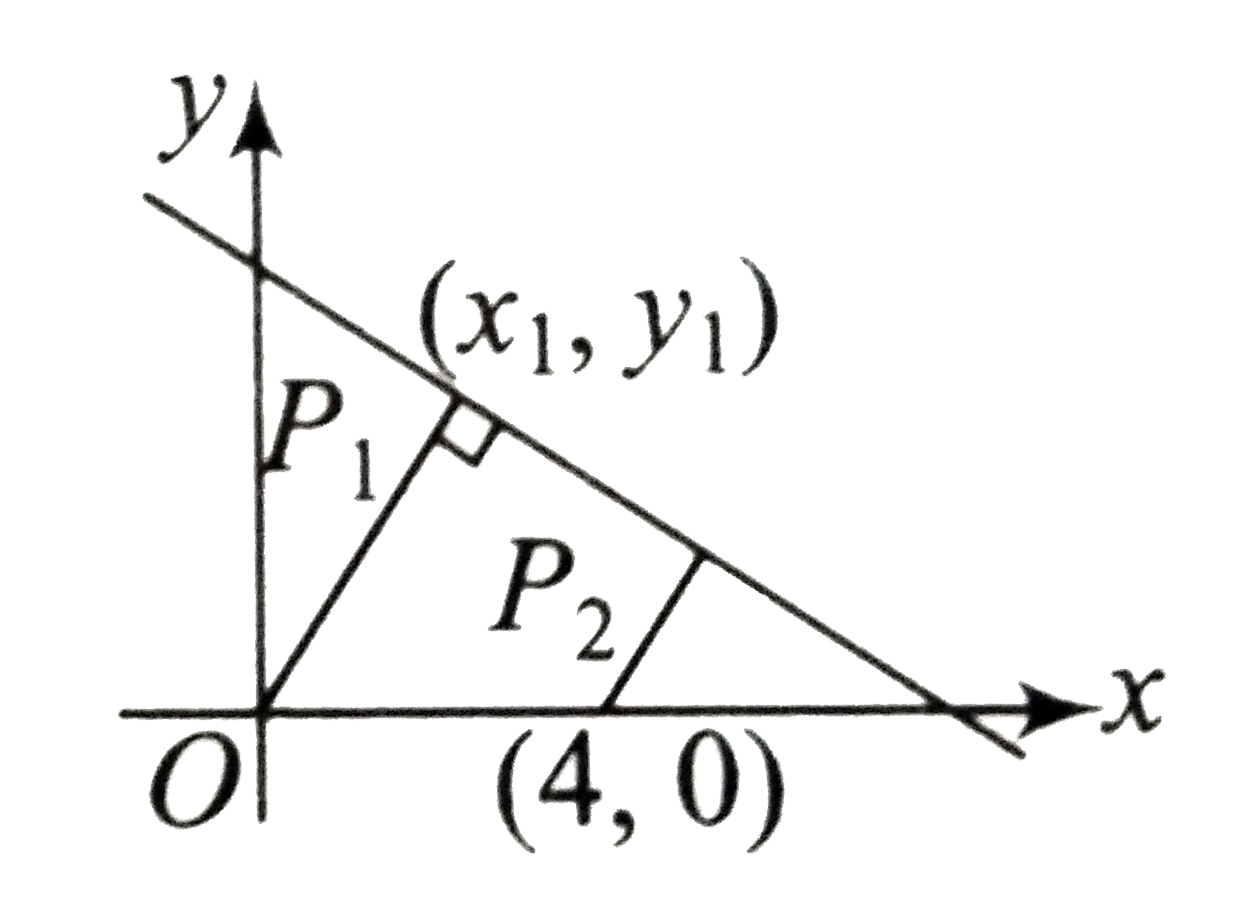
According to the equation,
p1p2=∣∣
∣∣x21+y21√x21+y21∣∣
∣∣∣∣
∣
∣∣4x1−(x21+y21)√x21+y21∣∣
∣
∣∣=9
i.e., ∣∣x21+y21−4x1∣∣=9
Locus is: x2+y2−4x−9=0
∴r2=4+9=13
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Multiple Correct Answers Type9videos
CIRCLES
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE6videos
CIRCLE
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - JEE Advanced Previous Year14videos
COMPLEX NUMBERS
Similar Questions
The line 3x+6y=k intersects the curve 2x2+3y2=1 at points AandB . The circle on AB as diameter passes through the origin. Then the value of k2 is__________
04:04View SolutionIn the diagram as shown, a circle is drawn with centre C(1, 1) and radius I and a line L. The line Lis tangential to the circle at Q. Further L meet the y-axis at R and the x-axis at Pis such a way that the angle OPQ equals θ where 0<θ<π2 The coordinates of Q are
07:35View SolutionFind the derivative of y=ln(cosx2).
02:15View SolutionLet z=x+iy be a complex number where xandy are integers. Then, the area of the rectangle whose vertices are the roots of the equation zz3+zz3=350 is 48 (b) 32 (c) 40 (d) 80
09:25View SolutionA variable line moves in such a way that the product of the perpendiculars from (4,0) and (0,0) is equal to 9. The locus of the feet of the perpendicular from (0,0) upon the variable line is a circle,the square of whose radius is
02:10View SolutionA variable line cuts pair of lines x^(2)-(a+b)x+ab=0 in such a way that intercept between subtends a right angle at origin.The locus of the foot of the perpendicular from origin on variable line is
05:13View SolutionFind the perpendicular distance from the origin of the perpendicular from the point (1,2) upon the straight line x−3y+4=0.
05:03View SolutionThe vertices of a triangle ABC are the points (0,b),(−a,0),(a,0). Find the locus of a point P which moves inside the triangle such that the product of perpendiculars from P to ABandAC is equal to the square of the perpendicular to BC.
04:45View SolutionIf the perpendicular distance of the line lx+my=1 from the point (0, 0) is a, then the diameter of the circle touching the given line and with centre (0, 0) is
02:11View SolutionFind the locus of the foot of the perpendicular from the point (a,0) to the straight line x−ty+at2=0 , t being variable.
09:09View SolutionThe algebraic sum of the perpendicular distances from A, B, C to a variable line is 0. Then the line passes through
06:48View SolutionIf the algebraic sum of the perpendicular distances from the points (2,0),(0,2),(4,4) to a variable line is equal to zero. Then the line passes through the point.
06:27View SolutionIf the algebraic sum of the perpendicular distances from the points (2, 0), (0, 2) and (1, 1) to a variable st. line be zero, then the line passes thro' the point :
07:43View SolutionA variable line moves in a plane such a way that the product of the perpendiculars from A(a, 0) and B(0, 0) is equal to λ2, A and B being on same side of variable line. The locus of the feet of the perpendicular from (0, 0) upon the variable line is a circle which has -
07:00View Solutiont একটি পরিবর্তনশীল চল হলে (a,0) বিন্দু থেকে x−ty+at2=0 সরলরেখার ওপর অঙ্কিত লম্বের পাদবিন্দুর সঞ্চারপথ নির্ণয় করাে।
05:43View SolutionA variable line moves in such a way that the product of the perpendiculars from (4, 0) and (0, 0) is equal to 9. The locus of the feet of the perpendicular from (0, 0) upon the variable line is a circle, the square of whose radius is
07:27View Solution

