The locus of the centre of a circle which cuts a given circle orthogonally and also touches a given straight line is (a) circle (c) parabola (b) line (d) ellipse
A
circle
B
line
C
parabola
D
ellipse
Text Solution
The correct Answer is:C
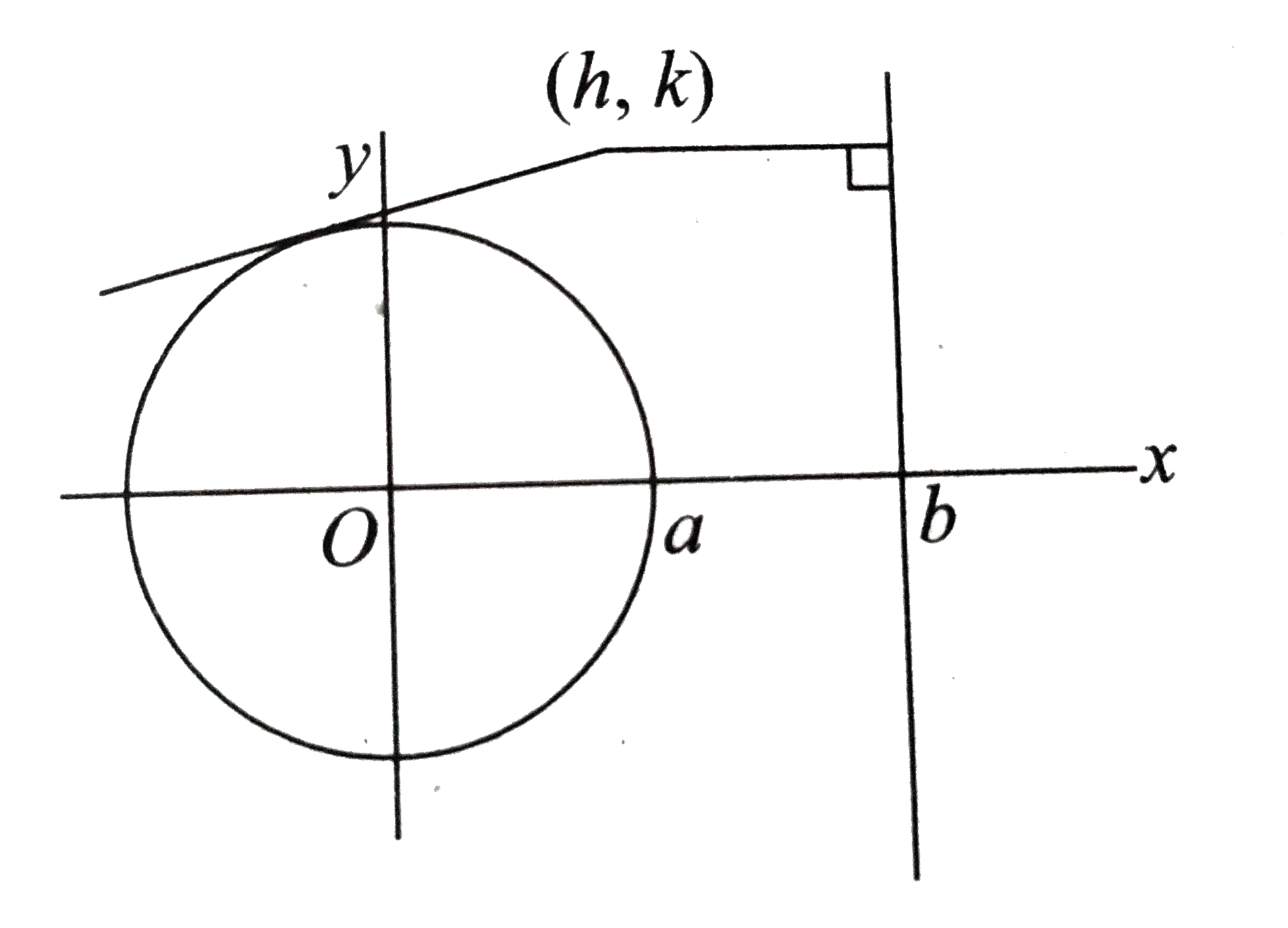
Without the loss of generality, the circle can be taken as x2+y2=a2 and the given line as x=b=0.
Let (h,k) be the centre of the required circle. Then length of tangent from (h,k) to the circle and distance of (h,k) from the line should be equal.
Hence, √h2+k2−a2=|h−b| or k2−a2=−2bh+b2
Thus, the locus is y2−a2=−2bx+b2.
i.e, y2=−2bx+b2+a2 which is a parabola.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Multiple Correct Answers Type9videos
CIRCLES
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE6videos
CIRCLE
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - JEE Advanced Previous Year14videos
COMPLEX NUMBERS
Similar Questions
Knowledge Check
- Question 1 - Select One
The locus of the centre of a circle the touches the given circle externally is a _______
AcurveBstraight lineCcircleDhelix - Question 2 - Select One
The locus of the centre of the circle that touch a given circle internally is ________
Astraight lineBhellixCcircleDNone of these
The locus of the centre of a circle the touches the given circle externally is a _______
View SolutionFind the locus of the centres of circles which touch a given line at a given point.
View SolutionProve that the locus of the center of the circle which touches the given circle externally and the given line is a parabola.
View SolutionThe locus of the centre of the circles which touches both the axes is given by
View SolutionThe locus of the centre of the circles which touches both the axes is given by
View SolutionThe locus of the point at which two given unequal circles subtend equal angles is: (A) a straight line(B) a circle (C) a parabola (D) an ellipse
View Solution

