Let A,B, and C be three sets such that
A={(x,y)∣xcosθ=ysinθ=5,where'θ'is parameter}
B={(x,y)∣x−3cosϕ=y−4sinϕ=r}
C={(x,y)∣(x−3)2+(y−4)2≤R2}
If ϕ is fixed and r varies and (A∩B)=1, then secϕ is equal to Solution in Tamil
54
−54
53
−53
The correct Answer is:2
A={(x,y)}xcosθ=ysinθ=5, where θ is parameter }
A is set of points which lie of the circle C1:x2+y2=25
B={(x,y)∣x−3cosϕ=y−4sinϕ=r}
Ifϕ varies and r is fixed, then B is the set of all points which lie on a circle C2:(x−3)2+(y−4)2=r2
And if ϕ is fixed and r varies, then B is the set of all points which lie on the straight line L:y−4=tanθ(x−3).
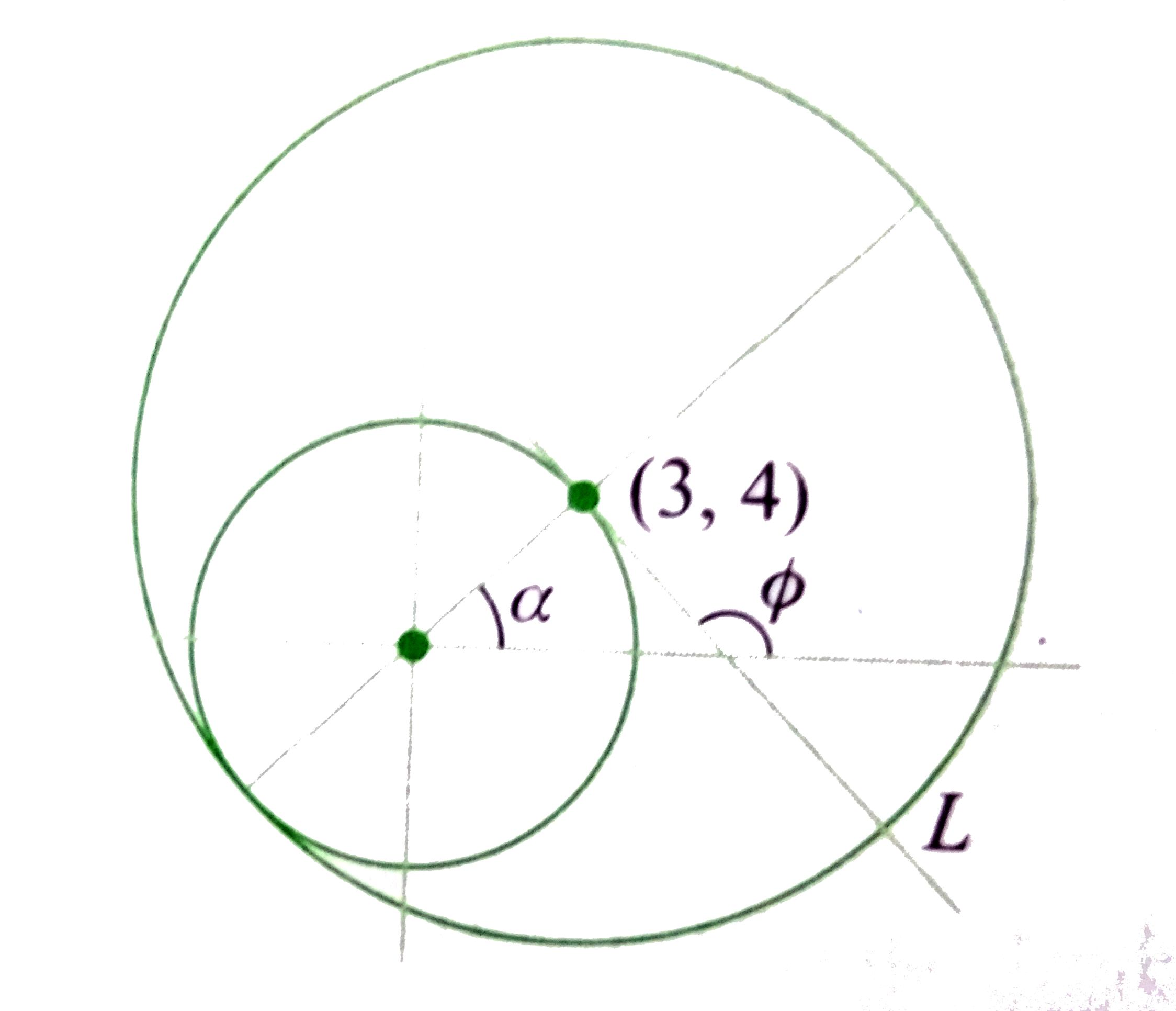
Now, if A∩C=A
Both circle C1 and C2 must touch each other internally.
So, R must be 10.
If ϕ is fixed and r varies and n(A∩B)=1, circle C1 touches line L.
ϕ=90∘+α
∴secϕ=sec(90∘+α)=−cosectα=−54
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Matrix)1videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Numerical)18videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)25videos
CIRCLE
- BOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
Similar Questions
Let C1 and C2 be two circles whose equations are x2+y2−2x=0 and x2+y2+2x=0 and P(λ,λ) is a variable point
View SolutionLet the lines (y−2)=m1(x−5) and (y+4)=m2(x−3) intersect at right angles at P (where m1andm2 are parameters). If the locus of P is x2+y2gx+fy+7=0 , then the value of |f+g| is__________
View Solutionabout to only mathematics
03:08View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' isView SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
07:00View SolutionLet A,B, and C be three sets such that
A={(x,y)∣xcosθ=ysinθ=5,where'θ'is parameter}
B={(x,y)∣x−3cosϕ=y−4sinϕ=r}
C={(x,y)∣(x−3)2+(y−4)2≤R2}
If A∩C=A, then minimum value of R is02:21View SolutionLet A,B, and C be three sets such that
A={(x,y)∣xcosθ=ysinθ=5,where'θ'is parameter}
B={(x,y)∣x−3cosϕ=y−4sinϕ=r}
C={(x,y)∣(x−3)2+(y−4)2≤R2}
If ϕ is fixed and r varies and (A∩B)=1, then secϕ is equal to06:43View SolutionIf x=rcosθcosϕ,y=rcosθsinϕ,z=rsinθ, then prove that x2+y2+z2=r2.
04:36View SolutionArea of the circle
x2+y2+2cosθsinϕ⋅x+2sinϕ⋅y−cos2ϕ=0 , is02:29View SolutionIfacosθsecϕ−xasin(θ+ϕ)=y−bsinθsecϕbcos(θ+ϕ)=tanϕ,show that,x2a2+y2b2=1.
02:34View Solutionযদি x=rcosθcosϕ, y=rcosθsinϕ এবং z=rsinθ হয়, তবে দেখাও যে , x2+y2+z2=r2
03:57View Solutionacosθsecϕ−xasin(θ+ϕ)=y−bsinθsecϕbcos(θ+ϕ)=tanϕ হলে দেখাও যে, x^2/a^2+y^2/b^2=1
07:40View SolutionFind the blanks.
(i) If x=acos3θ,y=bsin3θ then (xa)23+(yb)23=P––
(ii) if x=asecθcosϕ,y=bsecθsinϕ and z=ctanθ then x2a2+y2b2−z2c2=Q––
(iii) If cosA+cos2A=1,then sin2A+sin4A=R––05:52View SolutionIf x=asecθcosϕ,y=bsecθsinϕ,z=ctanθ, then, the value of x2a2+y2b2−z2c2 is :
03:35View SolutionIf x=rcosθsinϕ,y=rsinθsinϕ, and z=rcosϕ, prove that x2+y2+z2=r2.
06:19View SolutionLet A,B, and C be three sets such that
A={(x,y)∣xcosθ=ysinθ=5,where'θ'is parameter}
B={(x,y)∣x−3cosϕ=y−4sinϕ=r}
C={(x,y)∣(x−3)2+(y−4)2≤R2}
If A∩C=A, then minimum value of R is
(a)5
(b)6
(c)10
(d)1107:25View Solution

