In the given figure, there are two circles with centers A and B. The common tangent to the circles touches them, respectively,at P and Q. AR is 40cm and AB is divided by the point of contact of the circles in the ratio 5:3 What is the ratio of the length of AB to that of BR ?Solution in Tamil
1:4
2:3
2:5
7:4
The correct Answer is:2
r1r2=53=ARBR or BR=3×405=25 cm
ABBR=40−2424=1624=23
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Matrix)
1 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Numerical)
18 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
Similar Questions
Let C1 and C2 be two circles whose equations are x2+y2−2x=0 and x2+y2+2x=0 and P(λ,λ) is a variable point
View SolutionLet the lines (y−2)=m1(x−5) and (y+4)=m2(x−3) intersect at right angles at P (where m1andm2 are parameters). If the locus of P is x2+y2gx+fy+7=0 , then the value of |f+g| is__________
View Solutionabout to only mathematics
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionPerpendiculars are drawn, respectively, from the points PandQ to the chords of contact of the points QandP with respect to a circle. Prove that the ratio of the lengths of perpendiculars is equal to the ratio of the distances of the points PandQ from the center of the circles.
View SolutionA और B दो वृत्तों के केंद्र है जिनकी त्रिज्या क्रमश: 11 सेमी और 6 सेमी है, एक उभयनिष्ट अनुस्पर्शी रेखा दोनों वृत्तों का क्रमश: P और Q पर स्पर्श करती है। यदि AB=13 सेमी हो, तो PQ की लम्बाई बताइए ?
View SolutionIn the given figure, there are two circles with centers A and B. The common tangent to the circles touches them, respectively,at P and Q. AR is 40cm and AB is divided by the point of contact of the circles in the ratio 5:3 What is the ratio of the length of AB to that of BR ?
View SolutionIn the given figure, there are two circles with centers A and B. The common tangent to the circles touches them, respectively,at P and Q. AR is 40cm and AB is divided by the point of contact of the circles in the ratio 5:3

The radius of the circle with center B is
View SolutionIn the given figure, there are two circles with centers A and B. The common tangent to the circles touches them, respectively,at P and Q. AR is 40cm and AB is divided by the point of contact of the circles in the ratio 5:3
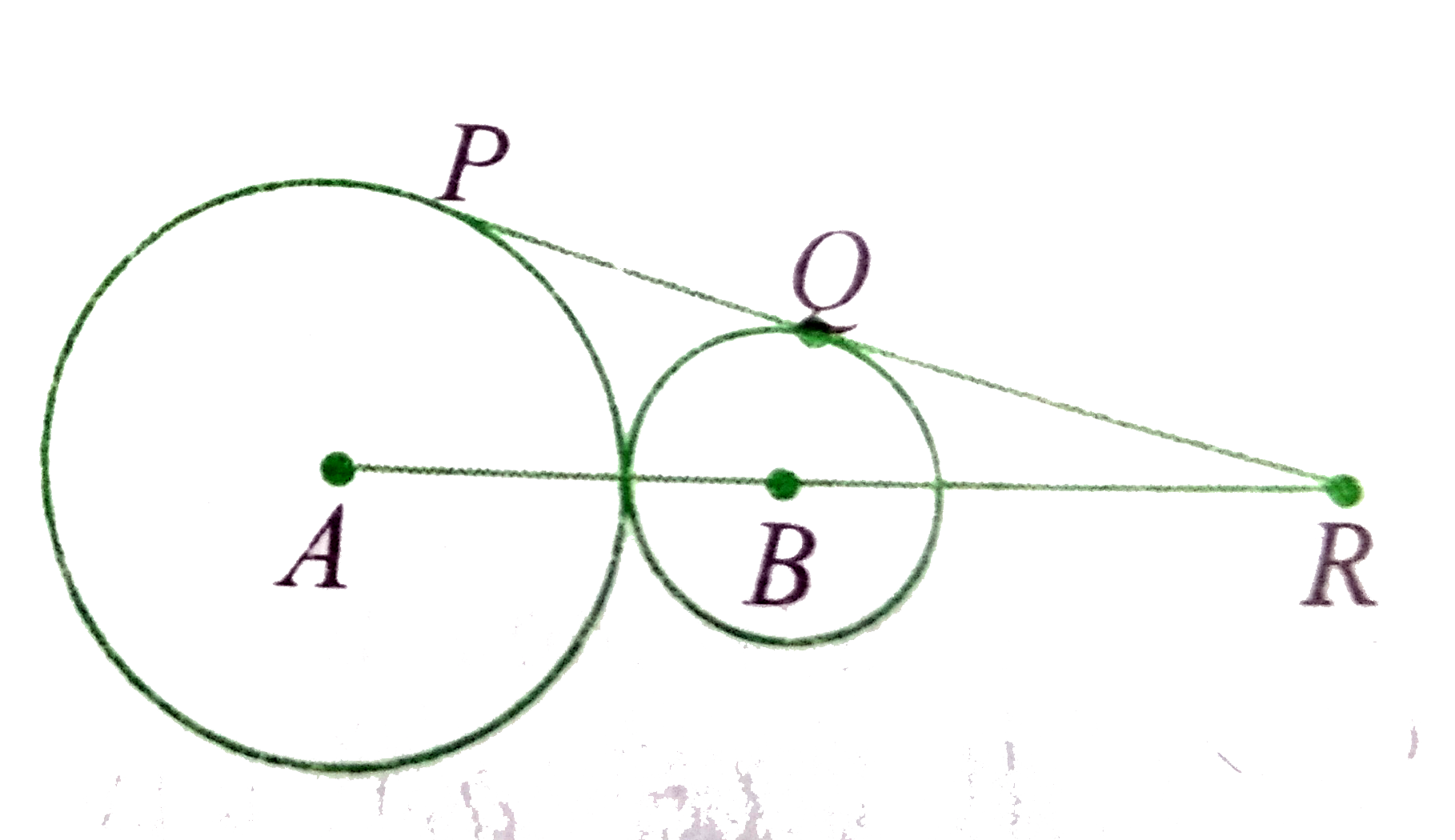
The length of QR is
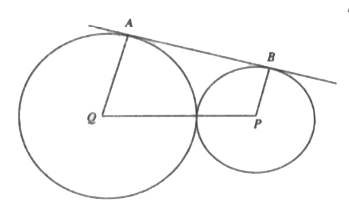
View SolutionColumn Ain the figure, P and Q are center of the two circle of radii 3 and 4 respectively. A and B are the points at which a common tangent touches each circleColumn BABPQ
View SolutionThe two circles intersect at C point. A common tangent of the two circles AB touches the two circles A and B. /_ Measurement of ACB
View SolutionIn the given figure, there are two circles with centers A and B. The common tangent to the circles touches them, respectively,at P and Q. AR is 40cm and AB is divided by the point of contact of the circles in the ratio 5:3

The radius of the circle with center B is
View SolutionA and B are the centers of two circles with radii 11 cm and 6 cm respectively. A common tangent touches these circles at P and Q respectively. If AB = 13 cm, then the length of PQ is:
View SolutionIn the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that:
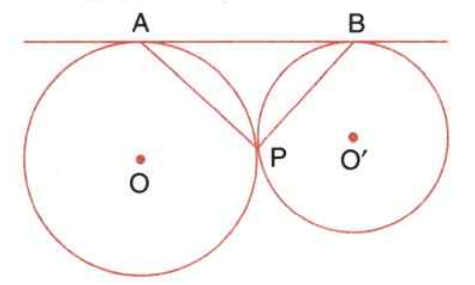
(i) tangent at point P bisects AB
(ii) angle APB=90∘
View Solution
