A circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QR, RP are D, E, F, respectively. The line PQ is given by the equation √3x+y−6=0 and the point D is (3 sqrt3/2, 3/2). Further, it is given that the origin and the centre of C are on the same side of the line PQ. The equation of circle C is Solution in Tamil
a)(x−2√3)2+(y−1)2=1
b)(x−2√3)2+(y+12)2=1
c)(x−√3)2+(y+1)2=1
d)(x−√3)2+(y−1)2=1
The correct Answer is:4
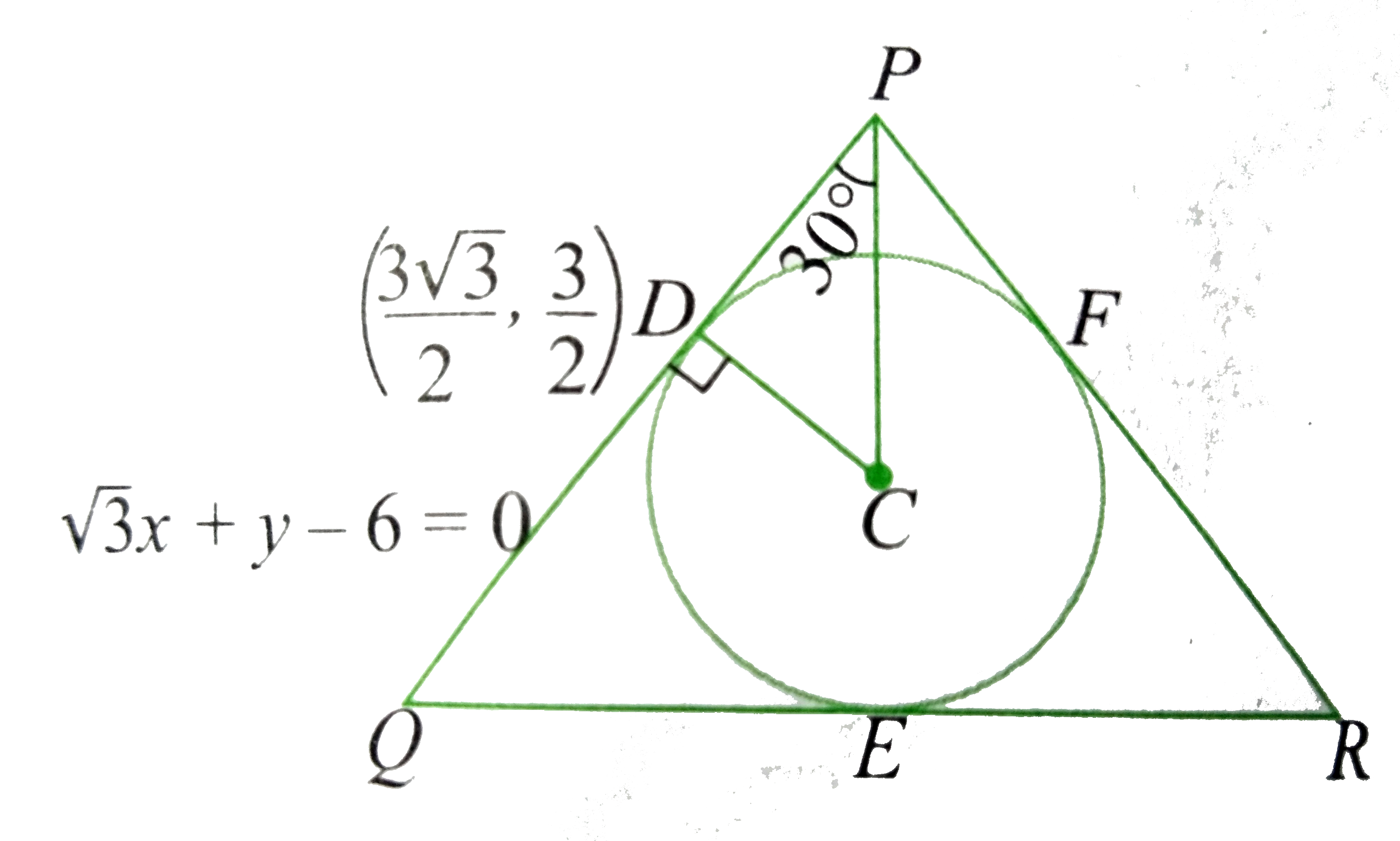
Equation of PQ is L1:√3x+y−6=0 (1)
Slope of PQ is −√3
∴Slope of CD is 1√3.
∴Equation of line CD in parametric from is
x−3√32cos30∘=y−32sin30∘=r
or x−3√32√32=y−3212=r
For centre C, r=±1
Two possible coordinates of centre are (2√3,2),(√3,1)
According to the question, center lies on the same side where origin lies with respect to line PQ.
Now L1(0,0)=−6<0
And L1(√3,1)=3+1−6<0
So Centre C must be (√3,1)
Hence, equation of the circle is (x−√3)2+(y−1)2=1
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Matrix)1videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Numerical)18videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)25videos
CIRCLE
- BOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
Similar Questions
Let C1 and C2 be two circles whose equations are x2+y2−2x=0 and x2+y2+2x=0 and P(λ,λ) is a variable point
19:32View SolutionLet the lines (y−2)=m1(x−5) and (y+4)=m2(x−3) intersect at right angles at P (where m1andm2 are parameters). If the locus of P is x2+y2gx+fy+7=0 , then the value of |f+g| is__________
19:32View Solutionabout to only mathematics
19:32View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is05:23View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
05:07View SolutionA circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ,QR,RPandD,E,F respectively. The line PQ is given by the equation √3+y−6=0 and the point D is (√32,32) The equation of circle C is : (A) (x−2√3)2+(y−1)2=1 (B) (x−2√3)2+(y+12)2=1 (C) (x−√3)2+(y+1)2=1 (D)(x−√3)2+(y−1)2=1
06:55View SolutionA circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ,QR,RPandD,E,F respectively. The line PQ is given by the equation √3+y−6=0 and the point D is (√32,32). Point E and F are given by : (A) (√32,32),(√3,0) (B) (√32,32),(√32,12) (C) (32,√32),(√32,12)
05:58View SolutionA circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ,QR,RPandD,E,F respectively. The line PQ is given by the equation √3+y−6=0 and the point D is (√32,32). Equation of the sides QR,RP are : (A) y=2√3x+1,y=2√3x−1 (B) y=1√3x,y=0 (C) y=√32x+1,y=√32x−1 (D) y=√3x,y=0
06:32View SolutionIn an isosceles triangle PQR, PQ =PR and S is any point on side QR. Then prove that: PQ2−PS2=QS×SR.
03:04View SolutionIf P(0,0,)Q(1,0)andR(12,√32) are three given points, then the centre of the circle for which the lines PQ,QR and RP are the tangents is
07:27View Solutionसमबाहु त्रिभुज PQR के अंतनिर्हित एक वृत C स्थित है जिसकी त्रिज्या 1 है। त्रिभुज की भुजाओ PQ, QR, RF को बिंदु D, E, F पर स्पर्श करता है। रेखा PQ का समीकरण √3x+y−6=0 तथा बिंदु D(3√32,32) है। यह भी दिया है की मूलबिंदु व C का केंद्र रेखा PQ के एक तरफ ही स्थित है।
वृत C का समीकरण है05:58View Solutionएक वृत्त जिसकी त्रिज्या 1 है। समबाहु त्रिभुज PQR के अन्दर स्थित है। भुजाओं PQ, QR, RP से वृत्त C के स्पर्श बिन्दु क्रमशः D,E, F हैं। रेखा PQ का समीकरण √3x+y−6=0 है तथा बिन्दु D(3√32,32) है। दिया है कि, मूलबिन्दु तथा C का केन्द्रबिन्दु रेखा PQ के एक ओर है।
बिन्दु E तथा F निम्न में से हैं06:32View Solutionसमबाहु त्रिभुज PQR के अंतनिर्हित एक वृत C स्थित है जिकी त्रिज्या 1 है। त्रिभुज की भुजाओ PQ, QR, RF तथा बिंदु D, E, F पर स्पर्श करता है। रेखा PQ का समाकरण √3x+y−6=0 तथा बिंदु D(3√32,32) है। यह भी दिया है की मूलबिंदु व् C का केंद्र PQ के एक तरफ ही स्थित है।
भुजाओं RP व् RQ के समीकरण होंगे04:48View SolutionS is any point on side QR of a ΔPQR. Show that PQ+QR+RP>2PS .
06:55View SolutionA circle whose radius is 1. The equilateral triangle is located inside the PQR. The tangent points of the circles C from the sides PQ, QR, RP are D, E, F respectively. Equation of line PQ sqrt(3)x +y-6 = 0 Is and point D((3sqrt(3))/(2),(3)/(2)) is. Given that, the point of origin and center of C is on one side of PQ. The equation of circle C is
06:32View SolutionA circle whose radius is 1. The equilateral triangle is located inside the PQR. The tangent points of the circles C from the sides PQ, QR, RP are D, E, F respectively. Equation of line PQ sqrt(3)x +y-6 = 0 Is and point D((3sqrt(3))/(2),(3)/(2)) is. Given that, the point of origin and center of C is on one side of PQ. Points E and F are from the following
05:39View Solution

