Consider the quadrationax2−bx+c=0,a,b,c∈N which has two distinct real roots belonging to the interval (1,2).
The least value of c is

A

4

B

6

C

7

D

5

Text Solution
Verified by Experts

The correct Answer is:2

az2−bx+c=0
Let f(x)=ax2−bx+cbe
the correspoding quadratic expression and α,β be the roots of f(x)=0.
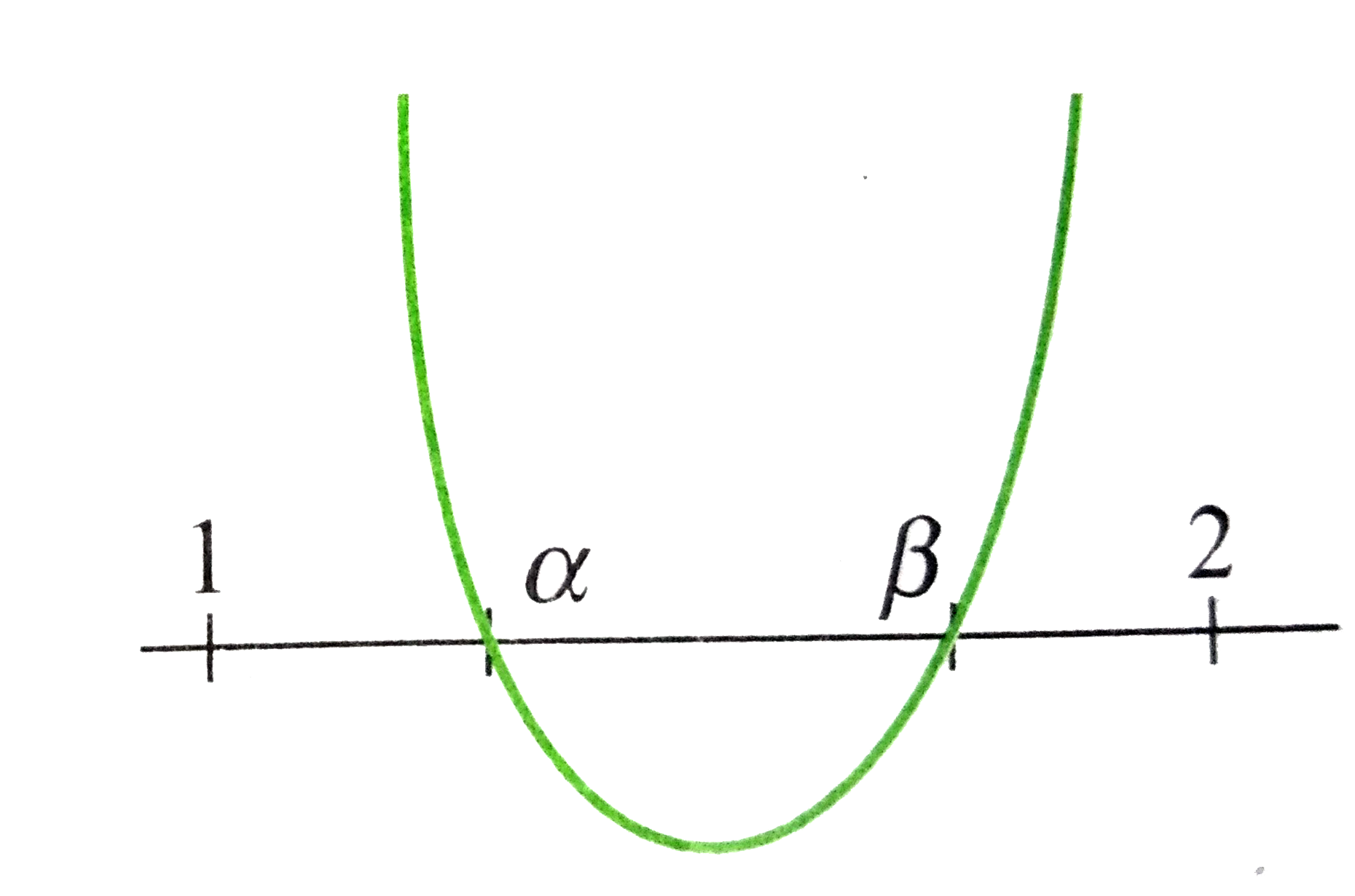
ocr_image
Then, f(x)=a(x−α)(x−β)
Now, af(1)>0,af(2)>0,1<b2a<2,b2−4ac>0
⇒a(1−α)(1−β)>0,a(2−α)(2−β)>0,2a<b<4a,b2−4ax>0
⇒a2(1−α)(1−β)(2−α)(2−β)>0
⇒a2(1−α)(1−β)(2−α)(2−β)>0
As f(x) and f(2) both are integers and f(1)>0, and f(2)>0, so
f(1)f(2)>0
⇒f(1)f(2)>1
⇒1≥a2(α−1)(2−α)(β−1)(2−β) (1)
Now, (α−1)+(2−α)2>((α−1)(2−α))1/2
⇒(α−1)(2−α)≤14
Similarly,
(β−1)(2−β)≤14
⇒(α−1)(2−α)(β−1)(2−β)<116
As α≠β, so α2>1 (Using (1))
⇒a>5
⇒b2>20candb>10⇒b≥11
Also, b2>100⇒c>5⇒c≥6

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12MATHSQUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Consider the quadrationax2−bx+c=0,a,b,c∈N which has two distinct real roots belonging to the interval (1,2).
    The least value of b is

    A10
    B11
    C13
    D15

  • Consider the quadrationax2−bx+c=0,a,b,c∈N which has two distinct real roots belonging to the interval (1,2).
    The least value of a is

    A4
    B6
    C7
    D5

  • If ax2+bx+c=0 have two distinct roots lying int eh interval (0,1),a,b,c εN The least value of b is

    A5
    B6
    C7
    D8