Let a vertical tower AB have its end A on the level ground. Let C be the mid-point of AB and P be a point on the ground such that AP = 2AB. If ∠BPC=β, then tan β is equal to Solution in Tamil
67
14
29
49
The correct Answer is:C
Let AB = h, then AP = 2h
and AC = B C = h2
Again, let ∠CPA=α
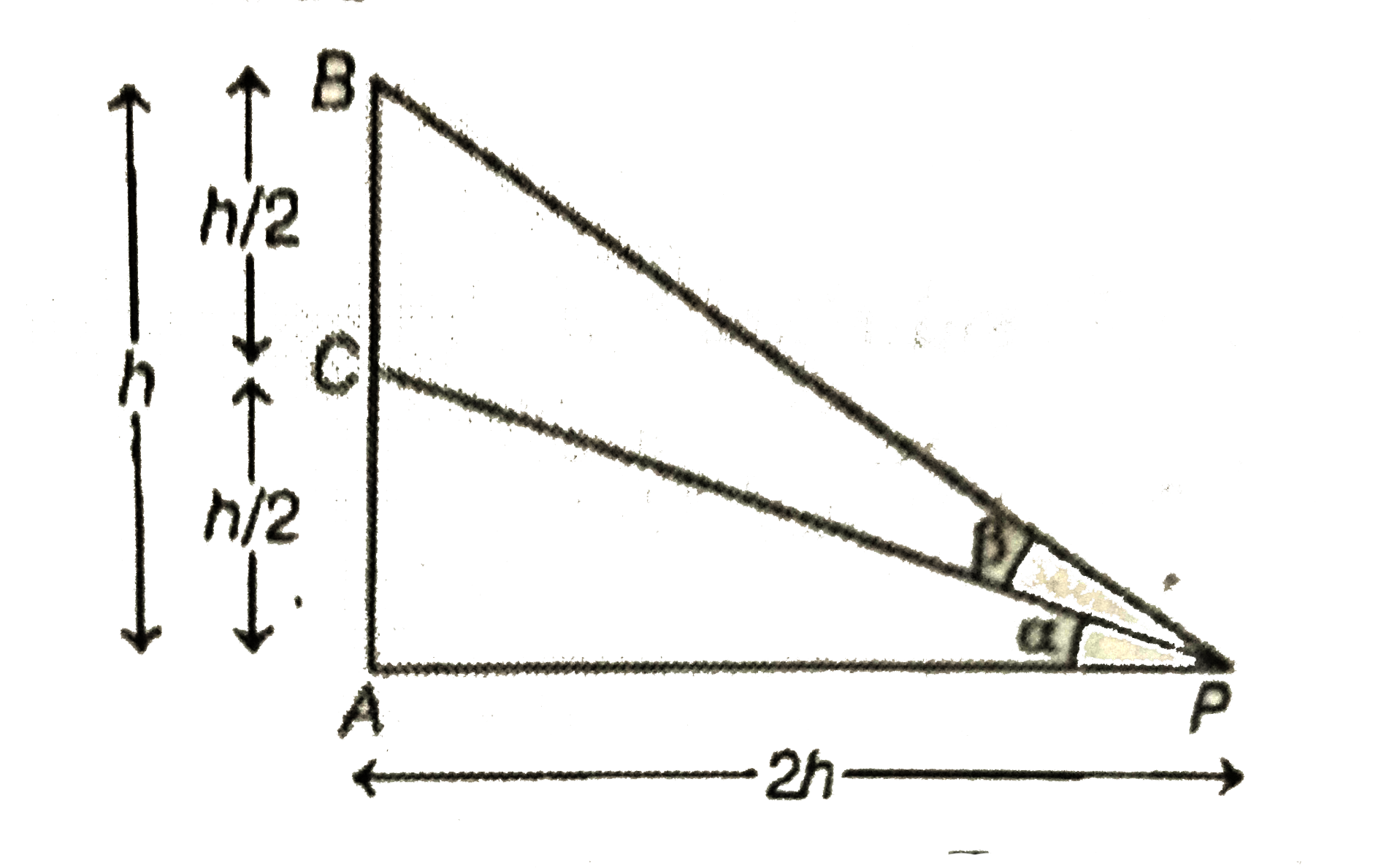
Now, in ∠ABP,tan(α+β)=ABAP=h2h=12
Also, in ΔACP,tanα=ACAP=22h=14
Now, tanβ=tan[(α+β)−α]
=tan(α+β)−tanα1+tan(α+β)tanα=12−141+12×14=1498=29
Similar Questions
AB is a vertical pole resting at the end A on the level ground. P is a point on the level ground such that AP = 3AB and C Is the midpoint of AB. If AC and CB subtend angles α and β, respectively, at P, then the value of tanβ is
02:28View SolutionLet a vertical tower AB have its end A on the level ground. Let C be the mid point of AB and P be a point on the ground such that AP=2AB. If ∠BPC=β, then tanβ is equal to : (1) 29 (2) 49 (3) 67 (4) 14
04:00View SolutionAB एक ऊर्ध्वाधर मीनार है बिंदु A जमीन पर है और C,AB का मध्य बिंदु है । भाग CB जमीन पर एक बिंदु P पर α कोण अंतरित करता है। यदि AP=nAB है तब सही संबंध है
11:22View SolutionAB is a vertical pole. The end A is on the level ground .C is the middle point of AB. P is a point on the level ground . The portion BC subtends an angles beta at P. If AP = nAB, then tan beta =
06:04View SolutionAB is a vertical pole resting at the end A on the level ground. P is a point on the level ground such that AP = 3AB and C Is the midpoint of AB. If AC and CB subtend angles α and β, respectively, at P, then the value of tanβ is
06:05View SolutionAB is a vertical pole resting at the end A on the level ground. P is a point on the level ground such that AP = 3AB and C Is the midpoint of AB. If AC and CB subtend angles alpha and beta , respectively, at P, then the value of tan beta is
03:53View SolutionLet a vertical tower A B have its end A on the level ground. Let C be the mid point of A B and P be a point on the ground such that A P=2A Bdot If /_B P C=beta, then tanbeta is equal to : (1) 2/9 (2) 4/9 (3) 6/7 (4) 1/4
02:45View Solution

