For the homogenous gaseous reaction A→3B, if pressure after time t was Pt and after completion of reaction, pressure was P∞ then select correct relation
a) k=1tln(P∞3(P∞−Pt))
b) k=1tln(2P∞(P∞−PT))
c) k=1tln(3P∞2P∞−Pt)
d) k=1tln(P∞3(P∞−PT))
Solution in Punjabi
k=1tin(P∞3(P∞−Pt))
k=1tin(2P∞(P∞−PT))
k=1tin(3P∞2P∞−Pt)
k=1tin(P∞3(P∞−PT))
The correct Answer is:D
Step by step video & image solution for For the homogenous gaseous reaction Ato3B, if pressure after time t was P_(t) and after completion of reaction, pressure was P_(oo) then select correct relation a) k=(1)/(t)"ln"((P_(oo))/(3(P_(oo)-P_(t)))) b) k=(1)/(t)"ln"((2P_(oo))/((P_(oo)-P_(T)))) c) k=(1)/(t)"ln"((3P_(oo))/(2P_(oo)-P_(t))) d) k=(1)/(t)"ln"((P_(oo))/(3(P_(oo)-P_(T)))) by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHEMICAL KINETIC & NUCLEAR CHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.3 To Q.32)
1 Videos
- CHEMICAL KINETIC & NUCLEAR CHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.33 To Q.62)
2 Videos
- SURFACE CHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - SURFACE CHEMISTRYEXERCISE - Level -2
1 Videos
Similar Questions
The following data pertain to reaction between A and B
S.No[A][B]RatemolL−1molL−1molL−1sec−1I1×10−22×10−22×10−4II2×10−22×10−24×10−4III2×10−24×10−28×10−4
Which of the following interference(s) can be drawn from the above data
(a) Rate constatnt of the reaction 10−4
(b) Rate law of reaction is k[A][B]
(c ) Rate of reaction increases four times on doubling the concentration of both the reactant Select the correct answer codes:
a) a,b and C
b) a and b
c) b and c
d) c alone
View Solutioncolumn Icolumn IIP.Zero order reaction1.t1/2α1[A]0Q.First order reaction2.t100%=[A]0/kR.second order reactions3.Involves at least two reactantsS.Pseudo unimolecular reaction4.[A]=[A]0e−kt
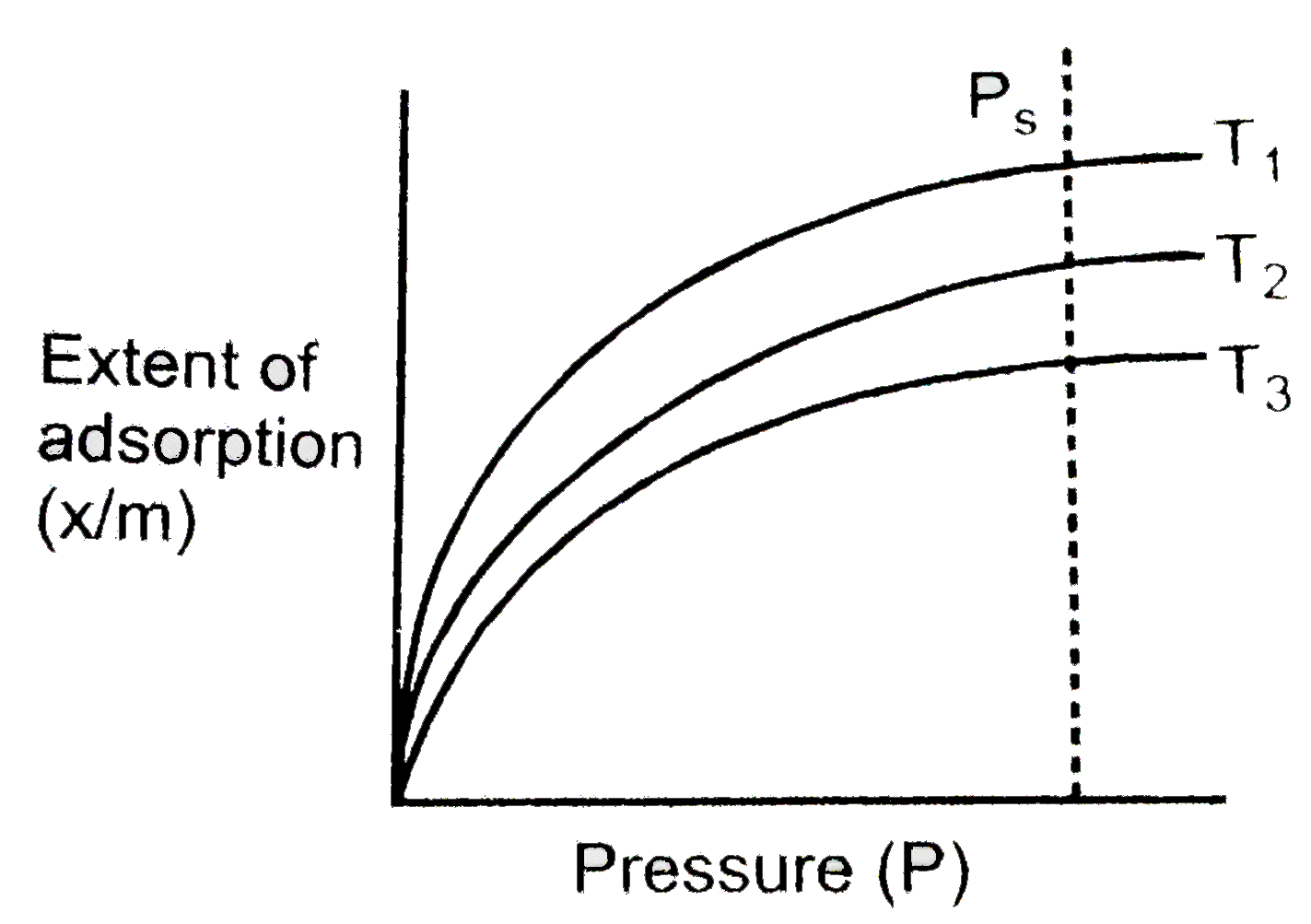
View Solutionfor the graph below, select correct order of temperture ?
View Solutionlet P1=⎡⎢⎣100010001⎤⎥⎦,P2=⎡⎢⎣100001010⎤⎥⎦,P3=⎡⎢⎣010100001⎤⎥⎦,P4=⎡⎢⎣010001100⎤⎥⎦,P5=⎡⎢⎣001100010⎤⎥⎦,P6=⎡⎢⎣001010100⎤⎥⎦ and X=6∑k=1Pk⎡⎢⎣213102321⎤⎥⎦PTk Where PTk is transpose of matrix Pk. Then which of the following options is/are correct?
View SolutionFor a first order homogeneous gaseous reaction
A→2B+C
if the total pressure after time t was P1 and after long time (t→∞) was P∞ then K in terms of Pt1 P∞ t is
View SolutionFor the homogenous gaseous reaction A→3B, if pressure after time t was Pt and after completion of reaction, pressure was P∞ then select correct relation
View SolutionFor a first order homogenous gaseous reaction, A→2B+C
then initial pressure was Pi while total pressure after time 't' was Pt. The right expression for the rate constants k in terms of Pi,Pt and t is :
View Solutionlimn→∞nPnn+1Pn+1−nPn=
View SolutionFor the reaction A(g)→B(g)+C(g) , the rate constant is given as (Pt is initial pressure and Pt is pressure at time t )-
View SolutionA→B+C Time t ∝
Total pressure of (B + C) P2 P3 Find k.
View SolutionFor a gas phase first order reaction,
A(g)→B(g)+2C(g)+D(g)
The initial pressure was P0 While pressure after 't' time becomes Pt (Pt>P0). The expression for the rate constant (K) would be
View SolutionFor a first order homogeneous gaseous reaction A→2B+C, if the total pressure after time t was Pt and after a long time (→→∞) was P∞ then k in terms of Pt,P∞ and t is
View SolutionFor the homogenous gaseous reaction A→3B, if pressure after time t was Pt and after completion of reaction, pressure was P∞ then select correct relation
View SolutionFor a first order homogenous gaseous reaction, Ato2B+C then initial pressure was P_(i) while total pressure after time 't' was P_(t) . The right expression for the rate constants k in terms of P_(i),P_(t) and t is :
View SolutionFor a first order homogeneous gaseous reaction Ato 2B+C if the total pressure after time t was P_(1) and after long time (t to infty) was P_(infty) then K in terms of P_(t_(1)) P_(infty) t is
View Solution
