Maximum Height|Questions|Cordinate Of A Particle After A Given Time T|

The velocity time graph of the motion of a car is given here.

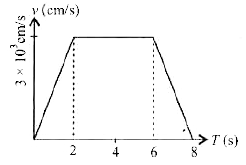AThe distance travelled by the car in the first six seconds is 150 m.
BThe deceleration of the car during the last two seconds are $- 15 \frac{m}{s^{2}}$ .
CThe distance travelled by the car in the first six second is 220 m.
DThe deceleration of the car during the last two second is $- 20 \frac{m}{s^{2}}$
A particle moves so that s=6+48t- $t^{3}$ . The direction of motion reverses after moving a distance of
A63
B104
C134
D288

Maximum Height|Questions|Cordinate Of A Particle After A Given Time T|Velocity And Direction Of Motion After A Given A Time