A uniformly tapering vessel is filled with a liquid of density 900kg/m3. The force that acts on the base of the vessel due to the liquid is (g=10ms−2) 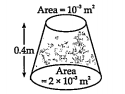 Solution in Marathi
Solution in Marathi
3.6 N
7.2 N
9.0 N
14.4 N
Step by step video & image solution for A uniformly tapering vessel is filled with a liquid of density 900 kg//m^3. The force that acts on the base of the vessel due to the liquid is (g=10 ms^-2) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A cube (side =10 cm ) of density 0.5 g//cm^(3) is placed in a vessel of base area 20 cmxx20 cm . A liquid of density 1.0 g//cm^(3) is gradually filled in the vessel at a constant rate Q=50 cm^(3)//s The cube will leave contact with the vessel after time t= ......... s.
View SolutionA similar shield vessel is placed as per the picture. The vessel is filled with a liquid whose density is 900 kg / m. There will be a force due to the fluid on the bottom of the vessel.
View Solutionएक बर्तन 425 लिटर तरल पदार्थ से पूरी तरह भरा हुआ था। इसमें से 8% तरल लिकेज व् वाष्पीकरण के कारण कम हो गया। बर्तन में तरल पद्धार्थ रह गया :
View SolutionA vessel contains water up to a height of 1.5 m. Taking the density of water 10^(3)kg m^(-3) , acceleration due to gravity 9.8 ms^(-2) and area of base of vessel 100 cm^(2) calculate : (a) the pressure and (b) the thrust, at the base of vessel.
View SolutionA liquid is filled upto a height of 20 m in a cylindrical vessel. The speed of liquid coming out of a small hole at the botton of the vessel is (take, g = 10 ms−2)
View SolutionA uniformly tapering vessel is filled with a liquid of of 1000kg//m^(3) . What is the force acting on the base of due to the liquid?
View SolutionThe height to which a cylindrical vessel is to be filled with a homogenous liquid, presses the side of the vessel equal to the force exerted by the liquid on the bottom of the vessel, is equal to
View SolutionA cylindrical vessel is filled with a liquid of density ρ to a height h such that the force exerted by the liquid on the bottom is equal to the force exerted on the walls of the vessel. Then h should be
View Solution
