A cylindrical vessel is filled with a liquid of density ρ to a height h such that the force exerted by the liquid on the bottom is equal to the force exerted on the walls of the vessel. Then h should be
equal to radius
more than the radius
less than the radius
two times the radius
The correct Answer is:A
Force exerted by the liquid on the bottom
F1= pressure × area =ρgh×πr2
The force exerted on the walls of the vessel.
F2=ρg(h2)×2πr×h [Mean pressure on the walls of the beaker is hρg2]
But F1=F2⇒ρghπr2=ρgh2πr∴h=r
Similar Questions
To what height should a cyclindrical vessel be filled with a homogeneous liquid to make the force with which the liquid pressure on the sides of the vessel equal to the force exerted by the liquid on the bottom of the vessel ?
View SolutionConsider a regular tank of size (l×b) filled with a liquid of density ρ to a height H as shown in figure. Find the force at the base and on the wall of the tank.

View Solution
Knowledge Check
A cylindrical vessel of radius r is filled with a homogeneous liquid upto a height h. It is found that the force exerted by the liquid column on the bottom of the cylinder is equal to the force exerted by the liquid on the sides of the cylinder. What is the relation between r and h?
Ar=h2Br=hCr=2hDr=32hTo what height should a cyclindrical vessel be filled with a homogeneous liquid to make the force with which the liquid pressure on the sides of the vessel equal to the force exerted by the liquid on the bottom of the vessel ?
Aequal to the radiusBless than radiusCmore than radiusDfour times of radiusTo what height should a cyclindrical vessel be filled with a homogeneous liquid to make the force with which the liquid pressure on the sides of the vessel equal to the force exerted by the liquid on the bottom of the vessel ?
Aequal to the radiusBless than radiusCmore than radiusDfour times of radius
Consider a regular tank of size (l×b) filled with a liquid of density ρ to a height H as shown in figure. Find the force at the base and on the wall of the tank.

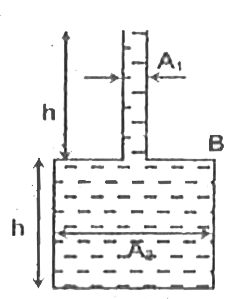
View SolutionThe vessel shown in the figure has two sections of area of cross - section A1andA2 .A liquid of density ρ fills both the section upto a height h in each . Consider atmospheric pressure P0 also . Find
(a) the pressure at the base of vessel .
(b) the force exerted by the liquid on the base of the vessel .
(c ) the downward force exerted by the walls of the vessel at the level B
View SolutionIn the following figure shown, a liquid is filled into the vessel up to a height h and the forces exerted against the liquid by the walls of the vessel are shown by arrows, the force being everywhere perpendicular to the walls of the vessel. For this situation mark out the correct statement(s).

View SolutionThe height to which a cylindrical vessel be filled with a homogenous liquid, to make the average force with which the liquid presses the side of the vessel equal to the force exerted by the liquid on the bottom of the vessel, is equal to.
View SolutionIn the following figure shown, a liquid is filled into the vessel up to a height h and the forces exerted against the liquid by the walls of the vessel are shown by arrows, the force being everywhere perpendicular to the walls of the vessel. For this situation mark out the correct statement(s).

View Solution
