रेषा AC व रेषा BD परस्परांना P बिंदूत छेदतात. 'm∠APD=47°',' ∠APB','∠BPC','∠CPD' यांची मापे लिहा.
Step by step video & image solution for रेषा AC व रेषा BD परस्परांना P बिंदूत छेदतात. 'm∠APD=47°',' ∠APB','∠BPC','∠CPD' यांची मापे लिहा. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
विस्तार करा :
(5a+6b)2
View Solutionपुढील सारणी पूर्ण करा :
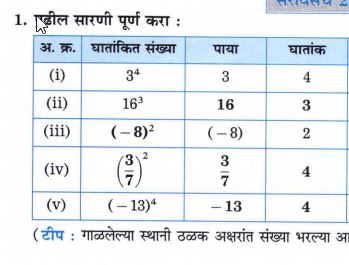
View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु P पर प्रतिच्छेद करते है दर्शाइए कि ar(APB)×ar(CPD)=ar(APD)×ar(BPC) है ।
View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते है। दर्शाइए कि
ar(APB)×ar(CPD)=ar(APD)×ar(BPC)
View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते है। दर्शाइए कि ar(APB)×ar(CPD)=ar(APD)×ar(BPC) है।
संकेत : A और C से BD पर लम्ब खींचिए
View SolutionIf the diagonals AC and BD intersect at point P in the cube in Figure what is the degree measure of angle APB ?
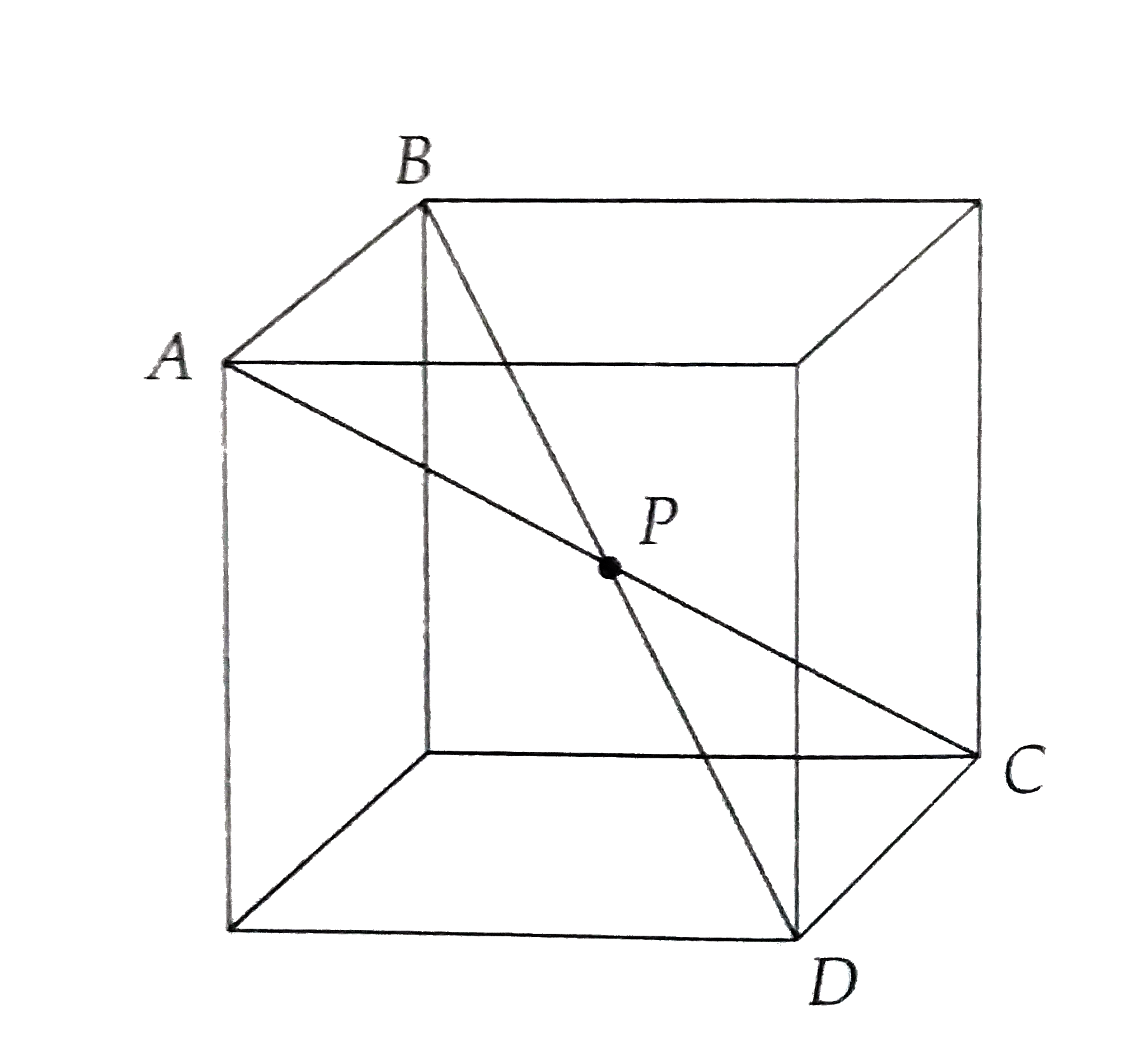
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPD).
[Hint : From A and C, draw perpendiculars to BD.
View SolutionDiagonals AC and BD of a quadrilateral ABCD each other at P. Show that ar (APB) × ar (CPD) =ar (APD) × ar (BPC)
View Solutionక్రింది పటంలో ABCD ఒక చతురస్రము మరియు ΔAPB ఒక సమబాహు త్రిభుజము అయిన ΔAPD≅ΔBPCఅని నిరూపించుము. (సూచన:ΔAPDΔBPC లలో ¯¯¯AD=¯¯¯BC,¯¯¯AP=¯¯¯BP మరియు ∠PAD=∠PBC=90∘−60∘=30∘)
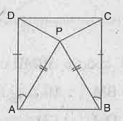
View SolutionIn the given figure, P is any point located in the interior of the parallelogram ABCD. Indicate that (i) ar (Delta APB ) + ar (Delta PCD ) = (1)/(2) (ar||^(g m)ABCD) (Ii) ar(Delta APD) + ar(Delta BPC ) = ar(Delta APB) + ar(Delta PCD)
View SolutionDiagonals AC and BD of quadrilateral ABCD intersect each other at P. Show that ar (APB)×ar(CPD) = ar (APD)×ar(BPC).
View Solutionਚਤੁਰਭੁਜ ABCD ਦੇ ਵਿਕਰਣ AC ਅਤੇ BD ਆਪਸ ਵਿਚ ਬਿੰਦੂ P 'ਤੇ ਕੱਟਦੇ ਹਨ। ਦਰਸਾਉ ਕਿ ar (APB) × ar (CPD) = ar (APD) × ar (BPC) ਹੈ। [ਸੰਕੇਤ: A ਅਤੇ C ਤੋਂ BD ਉੱਤੇ ਲੰਬ ਖਿੱਚੋ।
View SolutionIn the following diagrams, ABCD is a square and APB is an equilateral triangle. In each case,
(i) Prove that : ΔAPD≅ΔBPC
(ii) Find the angles of ΔDPC
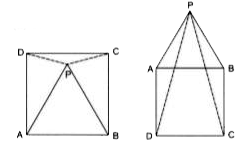
View SolutionLine AC and line BD intersect each other in the point P. m∠APD=47∘. Find the measures of ∠APB,∠BPC,∠CPD.
View SolutionIn trapezium ABCD, side AB is parallel to side DC. Diagonals AC and BD intersect at point P. Prove that triangles APD and BPC are equal in area.
View Solution
