State whether the statements are true (T) or false (F).
Two cylinders with equal volume will always have equal surface areas.
To determine whether the statement "Two cylinders with equal volume will always have equal surface areas" is true or false, we can analyze the relationship between the volume and surface area of cylinders.
1. Understanding the Volume of a Cylinder:
The volume V of a cylinder is given by the formula:
V=πr2h
where r is the radius of the base and h is the height of the cylinder.
2. Volume of Two Cylinders:
Let’s consider two cylinders:
- Cylinder 1 with radius r and height h
- Cylinder 2 with radius R and height H
According to the problem, their volumes are equal:
V1=V2⟹πr2h=πR2H
Simplifying this, we get:
r2h=R2H
3. Understanding the Surface Area of a Cylinder:
The total surface area A of a cylinder is given by the formula:
A=2πr(h+r)
Therefore, for both cylinders, we have:
- Surface area of Cylinder 1:
A1=2πr(h+r)
- Surface area of Cylinder 2:
A2=2πR(H+R)
4. Comparing Surface Areas:
To determine if the surface areas are equal, we need to check if:
2πr(h+r)=2πR(H+R)
This simplifies to:
r(h+r)=R(H+R)
5. Conclusion:
The equality r2h=R2H does not guarantee that r(h+r)=R(H+R). This means that two cylinders can have the same volume but different surface areas depending on the values of r,h,R, and H.
Therefore, the statement "Two cylinders with equal volume will always have equal surface areas" is False (F).
The volume V of a cylinder is given by the formula:
V=πr2h
where r is the radius of the base and h is the height of the cylinder.
Let’s consider two cylinders:
- Cylinder 1 with radius r and height h
- Cylinder 2 with radius R and height H
According to the problem, their volumes are equal:
V1=V2⟹πr2h=πR2H
Simplifying this, we get:
r2h=R2H
The total surface area A of a cylinder is given by the formula:
A=2πr(h+r)
Therefore, for both cylinders, we have:
- Surface area of Cylinder 1:
A1=2πr(h+r)
- Surface area of Cylinder 2:
A2=2πR(H+R)
To determine if the surface areas are equal, we need to check if:
2πr(h+r)=2πR(H+R)
This simplifies to:
r(h+r)=R(H+R)
The equality r2h=R2H does not guarantee that r(h+r)=R(H+R). This means that two cylinders can have the same volume but different surface areas depending on the values of r,h,R, and H.
Topper's Solved these Questions
- MENSURATIONBOOK - NCERT EXEMPLARCHAPTER - MENSURATIONEXERCISE - APPLICATIONS, GAMES AND PUZZLES
13 Videos
- MENSURATIONBOOK - NCERT EXEMPLARCHAPTER - MENSURATIONEXERCISE - THINK AND DISCUSS
2 Videos
- MENSURATIONBOOK - NCERT EXEMPLARCHAPTER - MENSURATIONEXERCISE - THINK AND DISCUSS
2 Videos
- LINEAR EQUATIONS IN ONE VARIABLEBOOK - NCERT EXEMPLARCHAPTER - LINEAR EQUATIONS IN ONE VARIABLEEXERCISE - THINK AND DISCUSS
3 Videos
- PLAYING WITH NUMBERS BOOK - NCERT EXEMPLARCHAPTER - PLAYING WITH NUMBERS EXERCISE - Think and Discuss
1 Videos
Similar Questions
Knowledge Check
State whether the following statements are true or false :
AAn electric motor converts mechanical energy into electrical energy.BAn electric generator works on the principle of electromagnetic induction.CThe field at the centre of a long circular coil carrying current will be parallel straight lines.DA wire with a green insulation is usually the live wire of an electric supply.
State whether the statements are true or falsea×b=b×a
View SolutionState whether the statements are true or falsea÷a=b÷a
View SolutionState whether the statements are true (T) or false (F).
1L = 1000 cm3
View SolutionState whether the statements are true (T) or (F) false.
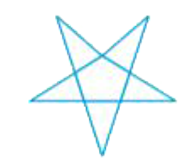 is a polygon.
is a polygon.
View Solutionstate whether the statement are true (T) or false (F).
 is a concave polygon.
is a concave polygon.
View SolutionState whether the statements are true or falsea÷(−b)=−(a÷b)
View Solutionstate whether the statement are true (T) or false (F).
Every kite is a trapezium.
View Solution
