State whether the statements are true (T) or false (F).
Ratio of area of a circle to the area of a square whose side equals radius of circle is 1:π.
To determine whether the statement "the ratio of the area of a circle to the area of a square whose side equals the radius of the circle is 1 : π" is true or false, we will follow these steps:
Step 1: Understand the formulas for the areas
- The area of a circle is given by the formula:
Area of Circle=πr2
where r is the radius of the circle.
- The area of a square is given by the formula:
Area of Square=side2
Since the side of the square is equal to the radius of the circle, we can write:
Area of Square=r2
Step 2: Calculate the ratio of the areas
- Now, we will find the ratio of the area of the circle to the area of the square:
Ratio=Area of CircleArea of Square=πr2r2
Step 3: Simplify the ratio
- When we simplify the ratio, the r2 terms cancel out:
Ratio=πr2r2=π
- Therefore, the ratio of the area of the circle to the area of the square is:
Ratio=π:1
Step 4: Compare with the statement
- The statement claims that the ratio is 1:π. However, we found that the ratio is π:1.
Conclusion
- Since the ratio we calculated is π:1 and not 1:π, the statement is false.
Final Answer
The given statement is False (F).
---
- The area of a circle is given by the formula:
Area of Circle=πr2
where r is the radius of the circle.
- The area of a square is given by the formula:
Area of Square=side2
Since the side of the square is equal to the radius of the circle, we can write:
Area of Square=r2
- Now, we will find the ratio of the area of the circle to the area of the square:
Ratio=Area of CircleArea of Square=πr2r2
- When we simplify the ratio, the r2 terms cancel out:
Ratio=πr2r2=π
- Therefore, the ratio of the area of the circle to the area of the square is:
Ratio=π:1
- The statement claims that the ratio is 1:π. However, we found that the ratio is π:1.
- Since the ratio we calculated is π:1 and not 1:π, the statement is false.
The given statement is False (F).
Topper's Solved these Questions
- MENSURATIONBOOK - NCERT EXEMPLARCHAPTER - MENSURATIONEXERCISE - APPLICATIONS, GAMES AND PUZZLES
13 Videos
- MENSURATIONBOOK - NCERT EXEMPLARCHAPTER - MENSURATIONEXERCISE - THINK AND DISCUSS
2 Videos
- MENSURATIONBOOK - NCERT EXEMPLARCHAPTER - MENSURATIONEXERCISE - THINK AND DISCUSS
2 Videos
- LINEAR EQUATIONS IN ONE VARIABLEBOOK - NCERT EXEMPLARCHAPTER - LINEAR EQUATIONS IN ONE VARIABLEEXERCISE - THINK AND DISCUSS
3 Videos
- PLAYING WITH NUMBERS BOOK - NCERT EXEMPLARCHAPTER - PLAYING WITH NUMBERS EXERCISE - Think and Discuss
1 Videos
Similar Questions
state whether the statement are true (T) or false (F).
 is a concave polygon.
is a concave polygon.
View SolutionState whether the statements are true (T) or (F) false.
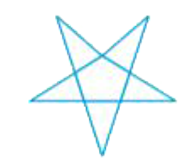 is a polygon.
is a polygon.
View Solutionstate whether the statement are true (T) or false (F).
 is a simple closed curve.
is a simple closed curve.
View SolutionState whether the statements are true (T) or false (F).
The areas of any two faces of a cube are equal.
View Solutionstate whether the statement are true (T) or false (F).
Every kite is a trapezium.
View SolutionState whether the statements are true (T) or false (F).
The areas of any two faces of a cuboid are equal.
View SolutionState whether the statements are true (T) or (F) false.
All kites are squares.
View SolutionState whether the statements are true (T) or (F) false.
 is a concave pentagon.
is a concave pentagon.
View SolutionState whether the statements are true (T) or (F) false.
All rhombuses are squares.
View SolutionState whether the statements are true (T) or (F) false.
All squares are rectangles.
View Solution
