State whether the statements are true (T) or false (F).
The surface area of a cube formed by cutting a cuboid of dimensions 2⋅1⋅1 in 2 equal parts is 2 sq. units.
To determine whether the statement is true or false, we need to analyze the given information step by step.
Step 1: Identify the dimensions of the cuboid
The dimensions of the cuboid are given as 2×1×1.
Step 2: Calculate the volume of the cuboid
The volume V of a cuboid is calculated using the formula:
V=length×width×height
Substituting the dimensions:
V=2×1×1=2 cubic units
Step 3: Cutting the cuboid into two equal parts
When the cuboid is cut into two equal parts, each part will have half the volume of the original cuboid:
Volume of each part=22=1 cubic unit
Step 4: Determine the shape of the parts
Since the question states that the cuboid is cut into two equal parts, we need to determine the shape of these parts. Each part will be a cube with a volume of 1 cubic unit.
Step 5: Calculate the side length of the cube
The volume V of a cube is given by:
V=a3
where a is the length of a side of the cube. Setting the volume to 1:
1=a3⟹a=1 unit
Step 6: Calculate the surface area of the cube
The surface area S of a cube is calculated using the formula:
S=6a2
Substituting the side length:
S=6×(1)2=6 square units
Conclusion
The statement claims that the surface area of the cube formed is 2 square units. However, we calculated that the surface area is 6 square units. Therefore, the statement is false.
Final Answer
The statement is False (F).
---
The dimensions of the cuboid are given as 2×1×1.
The volume V of a cuboid is calculated using the formula:
V=length×width×height
Substituting the dimensions:
V=2×1×1=2 cubic units
When the cuboid is cut into two equal parts, each part will have half the volume of the original cuboid:
Volume of each part=22=1 cubic unit
Since the question states that the cuboid is cut into two equal parts, we need to determine the shape of these parts. Each part will be a cube with a volume of 1 cubic unit.
The volume V of a cube is given by:
V=a3
where a is the length of a side of the cube. Setting the volume to 1:
1=a3⟹a=1 unit
The surface area S of a cube is calculated using the formula:
S=6a2
Substituting the side length:
S=6×(1)2=6 square units
The statement claims that the surface area of the cube formed is 2 square units. However, we calculated that the surface area is 6 square units. Therefore, the statement is false.
The statement is False (F).
Topper's Solved these Questions
- MENSURATIONBOOK - NCERT EXEMPLARCHAPTER - MENSURATIONEXERCISE - APPLICATIONS, GAMES AND PUZZLES
13 Videos
- MENSURATIONBOOK - NCERT EXEMPLARCHAPTER - MENSURATIONEXERCISE - THINK AND DISCUSS
2 Videos
- MENSURATIONBOOK - NCERT EXEMPLARCHAPTER - MENSURATIONEXERCISE - THINK AND DISCUSS
2 Videos
- LINEAR EQUATIONS IN ONE VARIABLEBOOK - NCERT EXEMPLARCHAPTER - LINEAR EQUATIONS IN ONE VARIABLEEXERCISE - THINK AND DISCUSS
3 Videos
- PLAYING WITH NUMBERS BOOK - NCERT EXEMPLARCHAPTER - PLAYING WITH NUMBERS EXERCISE - Think and Discuss
1 Videos
Similar Questions
State whether the statements are true (T) or false (F).
1L = 1000 cm3
View SolutionState whether the statements are true (T) or false (F).
The areas of any two faces of a cube are equal.
View Solutionstate whether the statement are true (T) or false (F).
 is a concave polygon.
is a concave polygon.
View SolutionState whether the statements are true (T) or (F) false.
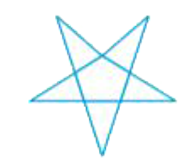 is a polygon.
is a polygon.
View Solutionstate whether the statement are true (T) or false (F).
 is a simple closed curve.
is a simple closed curve.
View SolutionState whether the statements are true (T) or false (F).
The areas of any two faces of a cuboid are equal.
View SolutionState whether the statements are true (T) or (F) false.
All kites are squares.
View Solutionstate whether the statement are true (T) or false (F).
Every kite is a trapezium.
View SolutionState whether the statements are true (T) or (F) false.
Every square is a rhombus.
View SolutionState whether the statements are true (T) or (F) false.
 is a concave pentagon.
is a concave pentagon.
View Solution
