The velocity of the CM of the system of particles can be represented as :
vCM=∑m1v1m1
vCM=m1v1M
vCM=∑m1v1M
None of the above
To find the velocity of the center of mass (CM) of a system of particles, we can follow these steps:
1. Understand the Definition: The center of mass (CM) of a system of particles is a point that represents the average position of the mass distribution in the system. The velocity of the center of mass is defined as the rate of change of its position with respect to time.
2. Position of the Center of Mass: The position of the center of mass Xcm for a system of n particles can be expressed as:
Xcm=m1x1+m2x2+…+mnxnM
where mi is the mass of the ith particle, xi is its position, and M is the total mass of the system given by M=m1+m2+…+mn.
3. Differentiate with Respect to Time: To find the velocity of the center of mass, we differentiate the position of the center of mass with respect to time:
Vcm=dXcmdt
4. Apply the Chain Rule: Using the chain rule, we differentiate the expression for Xcm:
Vcm=ddt(m1x1+m2x2+…+mnxnM)
Since M is constant (the total mass does not change), we can take it outside the differentiation:
Vcm=1Mddt(m1x1+m2x2+…+mnxn)
5. Differentiate Each Term: Now, we differentiate each term inside the summation:
Vcm=1M(m1dx1dt+m2dx2dt+…+mndxndt)
Here, dxidt represents the velocity vi of the ith particle.
6. Summation Form: We can rewrite the expression in summation notation:
Vcm=1Mn∑i=1mivi
7. Final Expression: Thus, the final expression for the velocity of the center of mass is:
Vcm=∑ni=1miviM
Conclusion:
The velocity of the center of mass of a system of particles is given by the formula:
Vcm=∑ni=1miviM
Xcm=m1x1+m2x2+…+mnxnM
where mi is the mass of the ith particle, xi is its position, and M is the total mass of the system given by M=m1+m2+…+mn.
Vcm=dXcmdt
Vcm=ddt(m1x1+m2x2+…+mnxnM)
Since M is constant (the total mass does not change), we can take it outside the differentiation:
Vcm=1Mddt(m1x1+m2x2+…+mnxn)
Vcm=1M(m1dx1dt+m2dx2dt+…+mndxndt)
Here, dxidt represents the velocity vi of the ith particle.
Vcm=1Mn∑i=1mivi
Vcm=∑ni=1miviM
The velocity of the center of mass of a system of particles is given by the formula:
Vcm=∑ni=1miviM
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - PHYSICS WALLAHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - NEET PAST 5 YEARS QUESTIONS
22 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - PHYSICS WALLAHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - NEET PAST 5 YEARS QUESTIONS
22 Videos
- SEMICONDUCTOR ELECTRONICS BOOK - PHYSICS WALLAHCHAPTER - SEMICONDUCTOR ELECTRONICS EXERCISE - NEET PAST 5 YEAR QUESTION
23 Videos
- THERMAL PROPERTIES OF MATTER BOOK - PHYSICS WALLAHCHAPTER - THERMAL PROPERTIES OF MATTER EXERCISE - NEET Past 5 Years Questions
12 Videos
Similar Questions
Knowledge Check
The velocity of the CM of the sytem of particle can be represented as :
AvCM=∑m1v1m1BvCM=m1v1MCvCM=∑m1v1MDNone of the aboveCM of the given system of particles will be at
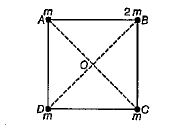 AODBOCCOBDAC
AODBOCCOBDACCM of the given system of particles will be at
 AODBOCCOBDAO
AODBOCCOBDAO
The reference frame, in which the centre of inertia of a given system of particles is at rest, translates with a velocity V relative to an inertial reference frame K. The mass of the system of particles equals m, and the total energy of the system in the frame of the centre of inertia is equal to ˜E. Find the total energy E of this system of particles in the reference frame K.
View SolutionIn a system of particles, internal forces can change:
View SolutionWrite an expression for the velocity of the centre of mass of a system of particles.
View SolutionNet external force acting on a system of particle is not equal to zero. If velocity and acceleration of the centre of mass of the system of particles at some instant of time are found to be v and a respectively select possible option (s).
View SolutionThe potential energy of the system is represented in the first figure. The force acting on the system will be represented by:
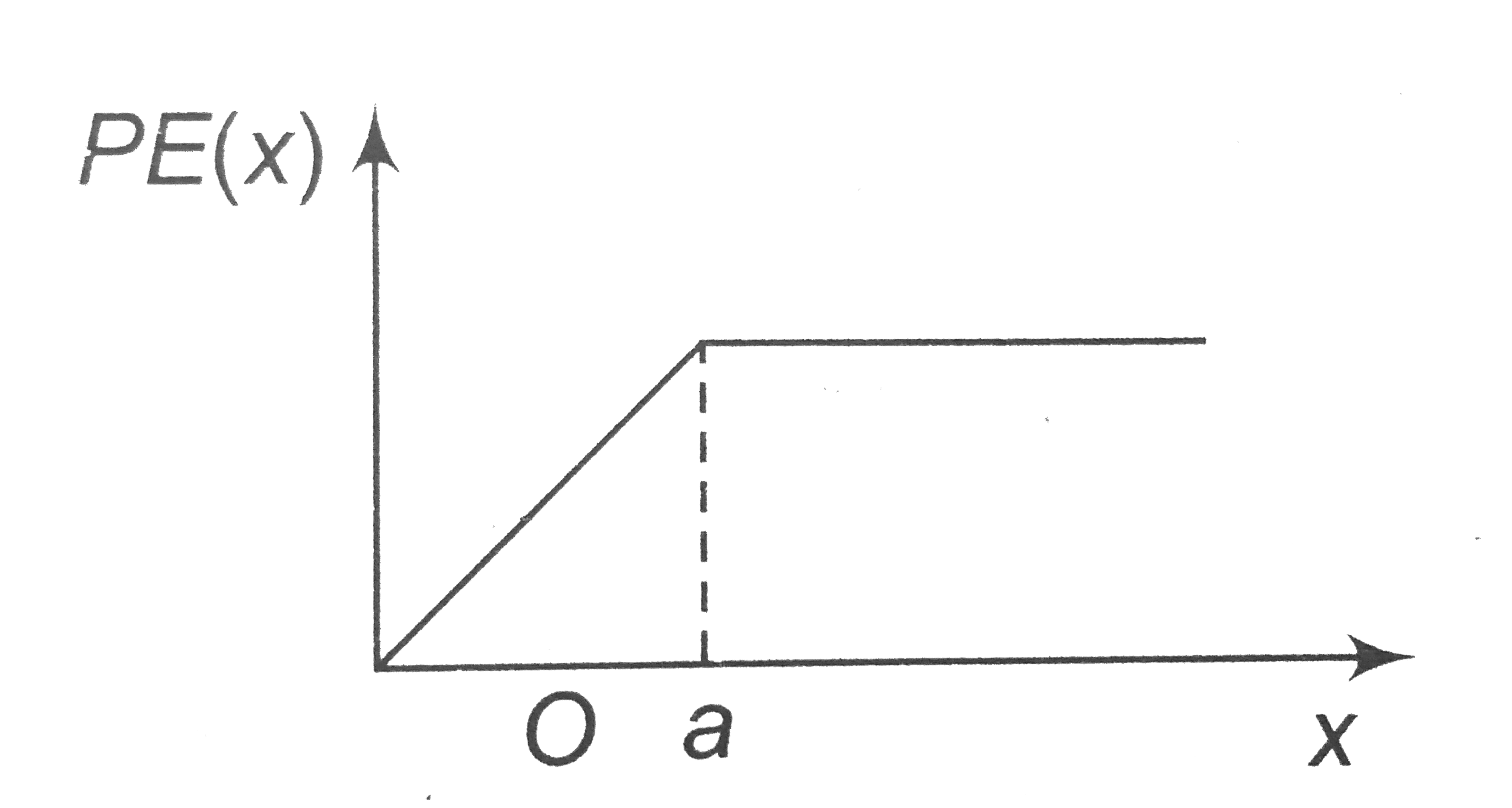
View Solution