AB is the diameter of a circle. C is a point on a tangent drawn on A. If AB = 24cm and AC = 7cm, then what is the length of BC?
AB एक वृत्त का व्यास है। C, A से खींची गई स्पर्शरेखा पर एक बिंदु
है,यदि AB = 24 cm और AC = 7 cm तो BC की लंबाई कया है
50 cm
15 cm
25 cm
26 cm
To solve the problem, we need to find the length of BC given that AB is the diameter of a circle, AC is a tangent to the circle at point A, and we know the lengths of AB and AC.
1. Identify the Given Values:
- Diameter AB = 24 cm
- Length of tangent AC = 7 cm
2. Determine the Radius of the Circle:
- The radius (r) of the circle is half of the diameter.
r=AB2=24 cm2=12 cm
3. Understand the Geometry:
- Since AC is a tangent to the circle at point A, and AB is the diameter, triangle ABC is a right triangle (by the tangent-secant theorem).
- Therefore, angle ABC = 90 degrees.
4. Apply the Pythagorean Theorem:
- In right triangle ABC, we can use the Pythagorean theorem:
BC2=AB2+AC2
5. Substitute the Known Values:
- Substitute AB = 24 cm and AC = 7 cm into the equation:
BC2=(24 cm)2+(7 cm)2
BC2=576 cm2+49 cm2
BC2=625 cm2
6. Calculate BC:
- Taking the square root of both sides:
BC=√625 cm2=25 cm
Final Answer:
The length of BC is 25 cm.
---
- Diameter AB = 24 cm
- Length of tangent AC = 7 cm
- The radius (r) of the circle is half of the diameter.
r=AB2=24 cm2=12 cm
- Since AC is a tangent to the circle at point A, and AB is the diameter, triangle ABC is a right triangle (by the tangent-secant theorem).
- Therefore, angle ABC = 90 degrees.
- In right triangle ABC, we can use the Pythagorean theorem:
BC2=AB2+AC2
- Substitute AB = 24 cm and AC = 7 cm into the equation:
BC2=(24 cm)2+(7 cm)2
BC2=576 cm2+49 cm2
BC2=625 cm2
- Taking the square root of both sides:
BC=√625 cm2=25 cm
The length of BC is 25 cm.
Topper's Solved these Questions
Similar Questions
In a circle with centre O, AD is a diameter and AC is a chord. Point B on AC such that OB = 7cm and ∠OBA=60∘. If ∠DOC=60∘, then what is the length of BC?
केंद्र वाले एक वृत्त में, AD एक व्यास है और AC एक जीवा है। AC पर एक बिंदु B इस प्रकार है की OB = 7 सेमी और ∠OBA=60∘ | यदि ∠DOC=60∘ है, तो BC की लंबाई क्या है?
View SolutionAB is the diameter of a circle with centre O. The tangent at a point C on the circle meets AB produced at Q. If ∠CAB=42∘, then what is the measure of ∠CQA?
AB एक वृत्त का व्यास है जिसका केंद्र O है | वत्त पर स्थित एक बिंदु C से गुजरने वाली स्पर्श रेखा AB से Q पर मिलती है | यदि ∠CAB=42∘ है, तो ∠CQA का मान क्या होगा ?
View Solution
Knowledge Check
△ABC is right-angled at A. If AB = 24 cm and AC = 7 cm, then BC = ?
A31 cmB17 cmC25 cmD28 cm
In the given figure. AB. AC and EF are tangents to a circle. If AC = 15 cm and DE = 3 cm. then the length of AE is:
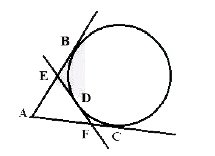
View SolutionIn the figure, chords AB and CD of a circle intersect externally at P. If AB = 4cm, CD =11cm and PD=15cm, then the length of PB is:
दी गयी आकृति में, जीवा AB और CD एक वृत्त को बाहरी रूप से P पर काटते हैं। यदि AB = 4cm, CD =11 cm और PD = 15cm है, तो PB की लंबाई ज्ञात करे |
View SolutionAB is a diameter of a circle with centre O. CB is a tangent to the circle at B. AC intersects the circle at G. If the radius of the circle is 6cm and AG = 8cm, then the length of BC is :
AB एक वृत्त का व्यास है जिसका केंद्र O है | CB, B पर वृत्त की स्पर्श रेखा है| AC, वृत्त को G पर काटता है | यदि वृत्त की त्रिज्या 6 सेमी है तथा AG = 8 सेमी है, तो BC की लंबाई ज्ञात करें |
View SolutionIn ∠ABC, AB=AC and D is a point on BC. If BD = 5cm, AB =12 cm and AD = 8 cm, then the length of CD is:
त्रिभुज ABC में, AB=AC है और D, BC पर स्थित एक बिंदु है | यदि BD =5 सेमी, AB = 12 सेमी और AD = 8 सेमी है, तो CD की लंबाई ज्ञात करें |
View SolutionTwo chords, AB and CD of circle meet at a point O, outside the circle. It is given that AB =7 cm, CD = 4 cm, OB = 5 cm. what is the length of OD?
किसी वृत्त की दो जीवाएं AB और CD, वृत के बाहर बिंदु O पर मिलती है|दिया गया है कि AB =7 cm, CD = 4 cm, OB = 5 cm तो OD क लंबाई क्या है?
View SolutionIn △ABC,the bisector of ∠A intersect side BC at D. If AB=12cm, AC =15cm and BC=18cm , then the length of BD is:
△ABC में, ∠A का द्विभाजक BC को D पर प्रतिच्छेदित करता है| यदि AB = 12cm, AC = 15cm और BC= 18cm है, तो BD की लंबाई है:
View SolutionChord AB of a circle is produced to a point P, and C is a point on the circle such that PC= 12cm, and BP = 10cm, then the length of AB (in cm ) is:
किसी वृत्त का जीवा ७8 को एक बिंदु P तक बढ़ाया जाता है, और C वृत्त पर एक बिंदु इस प्रकार है की PC=12cm, और BP = 10cm, फिर AB की लंबाई (सेमी में) है
View Solution