In a circle centred at O, a tangent AP is drawn from an external point A. If OA = 13 cm and OP = 5cm, then the length of tangent AP is:
O केंद्र वाले एक वृत्त में, एक स्पर्श रेखा AP को बाहरी बिंदु A से खींचा जाता है। यदि OA = 13 सेमी और OP = 5 सेमी है, तो स्पर्श रेखा AP की लंबाई ज्ञात करें
10 cm
8 cm
18 cm
12 cm
To find the length of the tangent AP from the external point A to the circle centered at O, we can use the Pythagorean theorem. Here are the steps to solve the problem:
1. Identify the Given Values:
- OA (the distance from point A to the center O of the circle) = 13 cm
- OP (the radius of the circle, which is the distance from O to the point P where the tangent touches the circle) = 5 cm
2. Understand the Geometry:
- In the right triangle AOP, where:
- OA is the hypotenuse,
- OP is one leg (the radius),
- AP is the other leg (the length of the tangent we want to find).
3. Apply the Pythagorean Theorem:
- According to the Pythagorean theorem:
OA2=OP2+AP2
- Substituting the known values:
132=52+AP2
4. Calculate the Squares:
- Calculate 132 and 52:
169=25+AP2
5. Rearrange the Equation:
- To find AP2, rearrange the equation:
AP2=169−25
AP2=144
6. Take the Square Root:
- Now, take the square root of both sides to find AP:
AP=√144=12 cm
Final Answer:
The length of the tangent AP is 12 cm.
---
- OA (the distance from point A to the center O of the circle) = 13 cm
- OP (the radius of the circle, which is the distance from O to the point P where the tangent touches the circle) = 5 cm
- In the right triangle AOP, where:
- OA is the hypotenuse,
- OP is one leg (the radius),
- AP is the other leg (the length of the tangent we want to find).
- According to the Pythagorean theorem:
OA2=OP2+AP2
- Substituting the known values:
132=52+AP2
- Calculate 132 and 52:
169=25+AP2
- To find AP2, rearrange the equation:
AP2=169−25
AP2=144
- Now, take the square root of both sides to find AP:
AP=√144=12 cm
The length of the tangent AP is 12 cm.
Topper's Solved these Questions
Similar Questions
A circle is centered at O. Two tangents AP and AQ are drawn from an external point A. If ∠POQ=118∘, then the ∠PAQ is:
एक वृत्त O पर केंद्रित है। दो स्पर्श रेखाएं AP और AQ बाह्य बिंदु A से खींचे गए हैं। यदि ∠POQ=118∘, फिर ∠PAQ = ?
View SolutionChords AB and CD of a circle intersect externally at P. If AB = 6 cm, CD = 3 cm and PB = 4 cm, then the length (in cm) of PD is :
एक वृत्त की जीवायें AB और CD एक दूसरे को बाहर से P पर काटती हैं | यदि AB = 6 सेमी,CD =3 सेमी और PB =4 सेमी है, तो PD की लंबाई (सेमी में ) ज्ञात करें |
View Solution
Knowledge Check
AC is a transverse common tangent to two circle with centres P and Q and radii 6 cm and 3 cm at the point A and C respectively.
If AC cuts PQ at the point B and AB = 8 cm, then the length of PQ is
P और Q केंद्र वाले दो वृत्तों की AC एक अनुप्रस्थ स्पर्श रेखा है। दोनों वृत्तों की A तथा C बिंदु पर त्रिज्या क्रमशः 6 सेमी. तथा 3 सेमी. है।
यदि AC, B बिन्दु पर PQ को काटती है और AB = 8 सेमी. है, तो PQ की लम्बाई ज्ञात करें।A12 cmB15 cmC13 cmD10 cm
In a circle centred at O, AB is a chord and C is any point on AB such that OC is perpendicular to AB. If the radius of the circle is 10 cm and OC = 6 cm, then the length of the chord is:
एक वृत्त में O केंद्र है , AB एक जीवा है और C, AB पर कोई बिंदु है जैसे OC, AB पर लंबवत है। यदि वृत्त की त्रिज्या 10 सेमी और OC = 6 सेमी है, तो जीवा की लंबाई ज्ञात करे |
View SolutionIn ∠ABC, AB=AC and D is a point on BC. If BD = 5cm, AB =12 cm and AD = 8 cm, then the length of CD is:
त्रिभुज ABC में, AB=AC है और D, BC पर स्थित एक बिंदु है | यदि BD =5 सेमी, AB = 12 सेमी और AD = 8 सेमी है, तो CD की लंबाई ज्ञात करें |
View SolutionIn a circle centred at O, AB is a chord and C is any point on AB, such that OC is perpendicular to AB. If the length of the chord is 16 cm and OC = 6 cm, the radius of circle is :
O केंद्र वाले एक वृत्त में, AB एक जीवा है और C, AB पर कोई बिंदु है, जैसे OC, AB पर लंबवत है। यदि जीवा की लंबाई 16 सेमी और OC = 6 सेमी है, तो वृत्त की त्रिज्या है:
View SolutionIn the figure, O is the centre of the circle of radius 29 cm, OP⊥AB,OQ⊥CD and AB is parallel to CD. If AB = 40 cm and CD = 42 cm, then the length of PQ is:
दी गयी आकृति में, O वृत्त का केंद्र है जिसकी त्रिज्या 29 सेमी है ,OP⊥AB,OQ⊥CD और AB, CD के समान्तर है। यदि AB= 40 सेमी और CD = 42 सेमी है, तो PQ की लंबाई है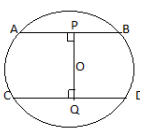
View SolutionIf two equal circles whose centres are O and intersect each o ′ other at the point A and B, OO′ =12 cm and AB= 16 cm, then radius of the circle is:
यदि दो बराबर वृत्त जिनके केंद्र O तथा o ′ हैं, एक-दूसरे को बिंदु A तथा B पर काटते हैं, तथा OO′ =12 सेमी एवं AB = 16 सेमी है, तो वृत्त की त्रिज्या ज्ञात करें |
View SolutionFrom an external point P, a tangent PQ is drawn to a circle, with centre O, touching the circle at Q. If the distance of P from the centre is 13 cm and the length of the tangent PQ is 12 cm, then the radius of the circle is:
एक बाहरी बिंदु P से, केंद्र O वाले एक वृत्त पर एक स्पर्श रेखा PQ खींची जाती है, जो वृत्त को Q पर स्पर्श करती है | यदि केंद्र से P की दूरी 13 सेमी है तथा स्पर्श रेखा PQ की लंबाई 12 सेमी है, तो वृत्त की त्रिज्या कितनी होगी ?
View SolutionAB is a diameter of a circle with centre O. CB is a tangent to the circle at B. AC intersects the circle at G. If the radius of the circle is 6cm and AG = 8cm, then the length of BC is :
AB एक वृत्त का व्यास है जिसका केंद्र O है | CB, B पर वृत्त की स्पर्श रेखा है| AC, वृत्त को G पर काटता है | यदि वृत्त की त्रिज्या 6 सेमी है तथा AG = 8 सेमी है, तो BC की लंबाई ज्ञात करें |
View Solution
