A unique circle can always be drawn through x number of given non-collinear points, then x must be: /
एक अद्वितीय वृत्त हमेशा x संख्या में दिए गए गैर-स॑रेखीय बिंदुओं से खींचा जा सकता है |x का मान होना चाहिए -
2
3
4
1
To solve the question of how many non-collinear points can define a unique circle, we can follow these steps:
1. Understanding Collinear and Non-Collinear Points:
- Collinear points are points that lie on the same straight line. Non-collinear points are points that do not all lie on the same line.
2. Analyzing One Point:
- If we have only one point, we can draw an infinite number of circles with that point as the center. Therefore, one point does not define a unique circle.
3. Analyzing Two Points:
- With two points, we can also draw an infinite number of circles. For example, we can take any point on the perpendicular bisector of the line segment joining the two points as the center of a circle. Thus, two points do not define a unique circle either.
4. Analyzing Three Non-Collinear Points:
- When we have three non-collinear points, we can draw exactly one unique circle that passes through all three points. This circle is known as the circumcircle of the triangle formed by the three points.
5. Conclusion:
- Therefore, the minimum number of non-collinear points required to define a unique circle is three.
Final Answer:
The value of x must be 3.
---
- Collinear points are points that lie on the same straight line. Non-collinear points are points that do not all lie on the same line.
- If we have only one point, we can draw an infinite number of circles with that point as the center. Therefore, one point does not define a unique circle.
- With two points, we can also draw an infinite number of circles. For example, we can take any point on the perpendicular bisector of the line segment joining the two points as the center of a circle. Thus, two points do not define a unique circle either.
- When we have three non-collinear points, we can draw exactly one unique circle that passes through all three points. This circle is known as the circumcircle of the triangle formed by the three points.
- Therefore, the minimum number of non-collinear points required to define a unique circle is three.
The value of x must be 3.
Topper's Solved these Questions
Similar Questions
The average of 18 numbers is 37.5. If six numbers of average x are added to them, then the average of all the numbers increases by one. The value of x is :
18 संख्याओं का औसत 37.5 है | यदि औसत x वाली छः संख्याओं को उनमें जोड़ा जाए, तो इन सभी संख्याओं का औसत एक से बढ़ जाता है | x का मान है :
View SolutionA secant is drawn from a point P to a circle P to a circle so that it meets the circle first at A, then goes through the centre, and leaves the circle at B. If the length of the tangent from P to the circle is 12 cm, and the radius of the circle is 5 cm, then the distance from P to A is:
एक छेदक रेखा को एक बिंदु P से एक वृत्त तक खींचा जाता है ताकि वह वत्त में पहले A से मिल जाए, फिर केंद्र से होकर जाता है, और B पर वृत्त छोड़ता है। यदि P से वृत्त की स्पश्रेखा की लंबाई है 12 सेमी, और वृत्त की त्रिज्या 5 सेमी है, फिर P से A की दूरी है:
View SolutionIf the given number 925x85 is divisible by 11, then the smallest value of x is:
यदि दी गयी संख्या 925x85 , 11 से विभाज्य है, तो x का सबसे छोटा मान कितना होगा ?
View SolutionIn the given figure XYZ is a secant and ZT is a tangent. What is the value of x.
दिए गए आकृति में XYZ एक छेदक रेखा है और ZT एक स्पर्शरेखा है। x का मान ज्ञात कीजिए।
View SolutionIn the following question, select the number which can be placed at the sign of question mark (?) from the given alternatives.
निम्नलिखित प्रश्न में, उस नंबर का चयन करें जिसे दिए गए विकत्यों में से प्रश्न चिह्न (?) के चिह्न पर रखा जा सकता है।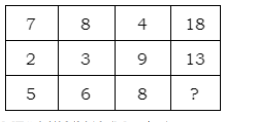
View SolutionIn the following question, select the number which can be placed at the sign of question mark (?) from the given alternatives.
निम्नलिखित प्रश्न में, उस नंबर का चयन करें जिसे दिए गए विकत्यों में से प्रश्न चिह्न (?) के चिह्न पर रखा जा सकता है।
View SolutionIn the following question, select the number which can be placed at the sign of question mark (?) from the given alternatives.
निम्नलिखित प्रश्न में, उस नंबर का चयन करें जिसे दिए गए विकत्यों में से प्रश्न चिह्न (?) के चिह्न पर रखा जा सकता है।
View SolutionIn the following question, select the number which can be placed at the sign of question mark (?) from the given alternatives.
निम्नलिखित प्रश्न में, उस नंबर का चयन करें जिसे दिए गए विकत्यों में से प्रश्न चिह्न (?) के चिह्न पर रखा जा सकता है।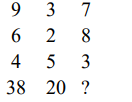
View SolutionIn the following question, select the number which can be placed at the sign of question mark (?) from the given alternatives.
निम्नलिखित प्रश्न में, उस नंबर का चयन करें जिसे दिए गए विकत्यों में से प्रश्न चिह्न (?) के चिह्न पर रखा जा सकता है।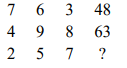
View SolutionIn the following question, select the number which can be placed at the sign of question mark (?) from the given alternatives.
निम्नलिखित प्रश्न में, उस नंबर का चयन करें जिसे दिए गए विकत्यों में से प्रश्न चिह्न (?) के चिह्न पर रखा जा सकता है।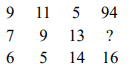
View Solution