The point A of a triangle ABC moves parallel to the straight line BC. Which one among the following also moves along a straight line parallel to BC?
एक त्रिभुज ABC का बिंदु A सीधी रेखा BC के समानांतर जाता है | निम्न में से कौन BC के समानांतर एक सीधी रेखा के साथ जाता है ?
a. The circumcentre
b. The centroid
c. The incentre
d. The orthocentre
To solve the problem, we need to analyze the movement of point A in triangle ABC and determine what else moves parallel to line BC when point A moves.
1. Understanding the Triangle:
Let's start by visualizing triangle ABC, where points A, B, and C are the vertices of the triangle.
Hint: Draw a triangle and label the vertices A, B, and C.
2. Identifying the Movement:
The problem states that point A moves parallel to line BC. This means that as point A shifts, it will maintain a constant distance from line BC.
Hint: Think about how a point can move parallel to a line while keeping its distance constant.
3. Understanding the Centroid:
The centroid (G) of a triangle is the point where the three medians intersect. A median connects a vertex to the midpoint of the opposite side. As point A moves, the centroid will also change its position.
Hint: Recall the definition of the centroid and how it is calculated based on the vertices of the triangle.
4. Analyzing the Movement of the Centroid:
When point A moves parallel to line BC, the positions of points B and C remain fixed. The centroid will move in a manner that keeps it aligned with the movement of point A. Since the centroid is dependent on the positions of all three vertices, it will also shift parallel to line BC.
Hint: Consider how the centroid's position is affected by the movement of point A.
5. Conclusion:
Therefore, as point A moves parallel to line BC, the centroid G of triangle ABC also moves along a straight line parallel to line BC.
Final Answer: The centroid of triangle ABC moves along a straight line parallel to BC.
Summary of Steps:
1. Visualize triangle ABC.
2. Identify the movement of point A.
3. Understand the concept of the centroid.
4. Analyze how the centroid moves with point A.
5. Conclude that the centroid moves parallel to line BC.
Let's start by visualizing triangle ABC, where points A, B, and C are the vertices of the triangle.
The problem states that point A moves parallel to line BC. This means that as point A shifts, it will maintain a constant distance from line BC.
The centroid (G) of a triangle is the point where the three medians intersect. A median connects a vertex to the midpoint of the opposite side. As point A moves, the centroid will also change its position.
When point A moves parallel to line BC, the positions of points B and C remain fixed. The centroid will move in a manner that keeps it aligned with the movement of point A. Since the centroid is dependent on the positions of all three vertices, it will also shift parallel to line BC.
Therefore, as point A moves parallel to line BC, the centroid G of triangle ABC also moves along a straight line parallel to line BC.
1. Visualize triangle ABC.
2. Identify the movement of point A.
3. Understand the concept of the centroid.
4. Analyze how the centroid moves with point A.
5. Conclude that the centroid moves parallel to line BC.
Topper's Solved these Questions
Similar Questions
The area of a △ABC is one unit. DE is a straight line parallel to BC , joining the points D and E on AB and AC respectively such that AD : DB = 1 : 6. The ratio of the areas of the triangles ADE and ABC is :
एक त्रिभुज ABC का क्षेत्रफल 1 इकाई है | DE, BC के समानांतर एक सीधी रेखा है जो क्रमशः AB और AC पर स्थित बिंदु D तथा E को इस प्रकार जोड़ती है कि AD : DB = 1 : 6 है | त्रिभुज ADE और ABC के क्षेत्रफल में अनुपात ज्ञात करें |
View SolutionIn a △ABC, the sides are AB= 16 cm, AC = 63cm, BC = 65cm. From A, a straight line AM is drawn up to the midpoint M of side BC. Then the length of AM is equal to :
त्रिभुज ABC में, AB = 16 सेमी, AC =63 सेमी, BC = 65 सेमी है | A से भुजा BC के मध्य बिंदु M तक एक सीधी रेखा AM खीची जाती है | AM की लंबाई ज्ञात करें |
View Solution
Knowledge Check
If the line joining the incentre to the centroid of a triangle ABC is parallel to the side BC. Which of the following are correct ?
A2b=a+cB2a=b+cCcotA2cotC2=3DcotB2cotC2=3If the line joining the incentre to the centroid of a triangle ABC is parallel to the side BC. Which of the following are correct ?
A2b=a+cB2a=b+cCcotA2cotC2=3DcotB2cotC2=3एक क्षार का मेथिल ऑरेंज को सूचक के रूप में उपयोग करते हुए एक अम्ल के साथ अनुमापन किया जाता है। निम्नलिखित में से कौन सा एक सही संयोजन है?
A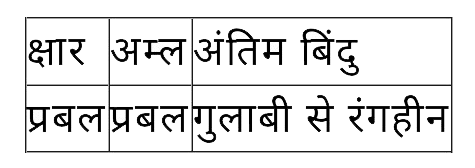 B
B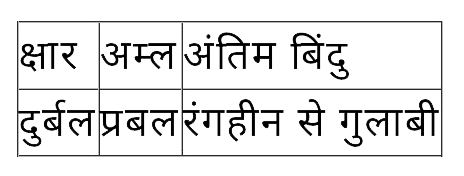 C
C D
D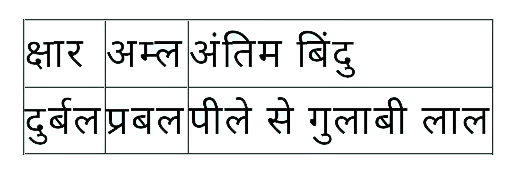
In a △ABC, the bisectors of ∠B and ∠C meet at point O within the triangle. If ∠A is given, then which among the given options is true?
एक △ABC में, ∠B और ∠C के समदविभाजक, त्रिभुज के भीतर बिंदु O पर मिलते हैं| अगर ∠A दिया गया है तो निम्नलिखित विकल्पों में से कौन सा सही है?
View SolutionIn a △ABC, the bisectors of ∠B and ∠C meet at point O within the triangle. If ∠BOC is given, then which among the given options is true?
एक △ABC में, ∠B और ∠C के समदविभाजक, त्रिभुज के भीतर बिंदु O पर मिलते हैं| अगर ∠BOC दिया गया है तो निम्नलिखित विकल्पों में से कौन सा सही है?
View SolutionThe side BC of a triangle ABC is extended to the point D. if ∠ACD=132∘ and ∠B=47∠A, then the measure of ∠A is equal to:
एक त्रिभुज ABC का भुजा BC बिंदु D तक बढ़ा दिया जाता है यदि ∠ACD=132∘ और ∠B=47∠A,तो ∠A का माप ज्ञात करे
View SolutionIn a triangle ABC, DE is parallel to BC, AD = a, DB = a+4, AE = 2a+3, EC = 7a. What is the value of ‘a’ if a>0?
एक त्रिभुज ABC में, DE, BC के समानांतर है | AD = a, DB = a+4, AE = 2a+3, EC = 7a है | यदि a>0 है, तो a का मान क्या होगा ?
View SolutionIn a circle with centre O, PQR is a tangent at the point Q on it. AB is a chord in the circle parallel to the tangent such that ∠BQR=70∘. What is the measure of ∠AQB ?
केंद्र O वाले एक वत्त में, PQR इस पर स्थित बिंदु Q पर एक स्पर्श रेखा है | AB वृत्त में एक जीवा है जो स्पर्श रेखा से इस प्रकार समानांतर है कि ∠BQR=70∘ है | ∠AQB का मान ज्ञात करें |
View Solution