A quadrilateral ABCD is inscribed in a circle with centre O.If ∠BOC=92∘ and ∠ADC=112∘ , then ∠ABO is equal to:
एक चतुर्भुज ABCD किसी वृत्त के भीतर स्थित है जिसका केंद्र O है | यदि ∠BOC=92∘ और ∠ADC=112∘ है, तो ∠ABO ज्ञात करें |
22∘
24∘
28∘
26∘
To solve the problem, we need to find the angle ∠ABO in the inscribed quadrilateral ABCD with given angles ∠BOC=92∘ and ∠ADC=112∘.
1. Understanding the Circle and Angles:
- Since ABCD is a cyclic quadrilateral, the angles subtended by the same arc are equal.
- The angle ∠BOC is the angle at the center of the circle, while ∠ABC and ∠ADC are the angles at the circumference.
2. Finding ∠AOB:
- The angle at the center ∠BOC is given as 92∘.
- The angle subtended at the circumference ∠ABC is half of the angle at the center:
∠ABC=12×∠BOC=12×92∘=46∘
3. Using the Property of Cyclic Quadrilaterals:
- In a cyclic quadrilateral, the sum of opposite angles is 180∘:
∠ABC+∠ADC=180∘
- We know ∠ADC=112∘. Therefore:
∠ABC+112∘=180∘
- Solving for ∠ABC:
∠ABC=180∘−112∘=68∘
4. Finding ∠AOB:
- Now, we can find ∠AOB using the relationship between ∠ABC and ∠AOB:
∠AOB=∠ABC+∠ABO
- We know ∠ABC=68∘ and ∠OBC (which is equal to ∠ABO) is 44∘ (as derived from the previous steps):
∠AOB=68∘+44∘=112∘
5. Finding ∠ABO:
- Now we can find ∠ABO:
∠ABO=∠AOB−∠ABC=112∘−68∘=24∘
Final Answer:
Thus, the value of ∠ABO is 24∘.
- Since ABCD is a cyclic quadrilateral, the angles subtended by the same arc are equal.
- The angle ∠BOC is the angle at the center of the circle, while ∠ABC and ∠ADC are the angles at the circumference.
- The angle at the center ∠BOC is given as 92∘.
- The angle subtended at the circumference ∠ABC is half of the angle at the center:
∠ABC=12×∠BOC=12×92∘=46∘
- In a cyclic quadrilateral, the sum of opposite angles is 180∘:
∠ABC+∠ADC=180∘
- We know ∠ADC=112∘. Therefore:
∠ABC+112∘=180∘
- Solving for ∠ABC:
∠ABC=180∘−112∘=68∘
- Now, we can find ∠AOB using the relationship between ∠ABC and ∠AOB:
∠AOB=∠ABC+∠ABO
- We know ∠ABC=68∘ and ∠OBC (which is equal to ∠ABO) is 44∘ (as derived from the previous steps):
∠AOB=68∘+44∘=112∘
- Now we can find ∠ABO:
∠ABO=∠AOB−∠ABC=112∘−68∘=24∘
Thus, the value of ∠ABO is 24∘.
Topper's Solved these Questions
Similar Questions
In a circle, chords AD and BC meet at a point E outside the circle. If ∠BAE=76∘ and ∠ADC=102∘, then ∠AEC is equal to:
एक वृत्त में, जीवाएं AD और BC वृत्त के बाहर स्थित बिंदु E पर मिलती हैं | यदि ∠BAE=76∘ और ∠ADC=102∘है, तो ∠AEC किसके बराबर है?
View SolutionIn the given figure, O is the centre of the circle. If ∠BAO=30∘ and ∠BCO=50∘, then ∠AOC is equal to:
दिए गए आकृति में, O वृत्त का केंद्र है। यदि ∠BAO=30∘ और ∠BCO=50∘, तो ∠AOC का मान है :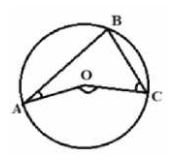
View SolutionA triangle ABC is inscribed in a circle with centre O. AO is produced to meet the circle at K and AD⊥BC. If ∠B=80∘ and ∠C=64∘, then the measure of ∠DAK is :
एक त्रिभुज ABC किसी वृत्त में अंतर्निहित है जिसका केंद्र O है | AO को बढ़ाया जाता है जो वृत्त से K पर मिलता है और AD⊥BC है | यदि ∠B=80∘ और ∠C=64∘ है, तो ∠DAK का माप क्या होगा ?
View SolutionAB is a diameter of a circle with centre O, and P is a point on the circle. If ∠POA=130∘, the ∠PBO is equal to:
AB केंद्र O के साथ एक वृत्त पर एक व्यास है, और P वृत्त का एक बिंदु है। यदि ∠POA=130∘, तो ∠PBO का मान ज्ञात करे|
View SolutionTwo chords AB and CD of a circle with centre O intersect each other at P If ∠APC=95∘ and ∠AOD=110∘, then what ∠BOC is:
केंद्र O वाले एक वृत्त की दो जीवाएँ AB तथा CD हैं जो एक-दूसरे को P पर प्रतिच्छेद करती हैं | यदि ∠APC=95∘ तथा ∠AOD=110∘है ,तो ∠BOC का मान क्या होगा ?
View SolutionPA and PB are tangents to a circle with centre O, from a point P outside the circle, and A and B are points on the circle. If ∠APB=40∘, then ∠OAB is equal to:
PA तथा PB एक वृत्त के बाहर स्थित बिंदु P से वृत्त की स्पर्श रेखाएं हैं जिसका केंद्र O है तथा A और B वृत्त पर स्थित बिंदु हैं | यदि ∠APB=40∘ है, तो ∠OAB का मान ज्ञात करें |
View SolutionPA and PB are the tangents to a circle with centre O, from a point P outside the circle. A and B are the points on the circle. If ∠APB=72∘,then ∠OAB is equal to:
PA तथा PB एक वृत्त पर वृत्त के बाहर स्थित बिंदु P से खींची गयी स्पर्श रेखाएं हैं जिसका केंद्र O है | A तथा B वृत्त पर स्थित बिंदु हैं | यदि ∠APB=72∘ है, तो ∠OAB का मान ज्ञात करें |
View SolutionIn a quadrilateral ABCD, E is a point in the interior of the quadrilateral such that DE and CE are the bisector of ∠D and ∠C, respectively, If ∠B=82∘ and ∠DEC=80∘ then ∠A= ?
एक चतुर्भुज ABCD में, E, चतुर्भुज के भीतरी भाग का एक बिंदु इस प्रकार है की DE और CE क्रमश ∠D और ∠C, के द्विभाजक हैं, यदि ∠B=82∘और ∠DEC=80∘ तो ∠A = ?
View SolutionABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and angle ADC = 125∘. Then ∠BAC is equal to:
ABCD एक चक्रीय चतुर्भज है जो इस प्रकार है कि AB इसे घेरने वाले वृत्त का व्यास है तथा कोण ADC = 125∘, है | कोण ∠BAC का मान ज्ञात करें |
View SolutionABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC=126∘. ∠BAC is equal to:
ABCD एक चक्रीय चतुर्भज है। जिसमें AB इसपर बने वृत्त का व्यास है और ∠ADC=126∘ है। ∠BAC बराबर है:
View Solution