In a circle with centre O, AB is the diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=25∘ , then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB व्यास है तथा CD एक ऐसी जीवा है कि ABCD एक समलम्ब बन जाता है | यदि ∠BAC=25∘ है, तो ∠CAD का मान ज्ञात करें |
45∘
65∘
40∘
25∘
To solve the problem, we need to find the measure of angle CAD in the trapezium ABCD, where AB is the diameter of the circle and CD is a chord. Given that angle BAC = 25°, we can follow these steps:
1. Identify the Given Information:
- AB is the diameter of the circle.
- CD is a chord.
- Angle BAC = 25°.
2. Draw the Circle and Mark Points:
- Draw a circle with center O.
- Mark points A and B on the circle such that AB is the diameter.
- Mark points C and D on the circle such that CD is a chord.
3. Understand the Properties of Angles:
- Since AB is the diameter, angle ADB (where D is on the circle) will be 90° (angle in a semicircle).
- Therefore, angle ADB = 90°.
4. Use the Inscribed Angle Theorem:
- The angle BAC is subtended by the chord BC at point A. By the inscribed angle theorem, the angle BDC (subtended by the same chord BC at point D) will also be equal to angle BAC.
- Thus, angle BDC = angle BAC = 25°.
5. Identify the Angles in Triangle ADB:
- In triangle ADB, we have:
- angle ADB = 90°
- angle BAC = 25°
- Let angle CAD = x (the angle we need to find).
6. Apply the Angle Sum Property:
- The sum of angles in triangle ADB is 180°.
- Therefore, we can write the equation:
angleADB+angleBAC+angleCAD=180°
- Substituting the known values:
90°+25°+x=180°
7. Solve for x:
- Combine the known angles:
115°+x=180°
- Rearranging gives:
x=180°−115°=65°
8. Conclusion:
- Therefore, angle CAD = 65°.
Final Answer:
angle CAD=65°
- AB is the diameter of the circle.
- CD is a chord.
- Angle BAC = 25°.
- Draw a circle with center O.
- Mark points A and B on the circle such that AB is the diameter.
- Mark points C and D on the circle such that CD is a chord.
- Since AB is the diameter, angle ADB (where D is on the circle) will be 90° (angle in a semicircle).
- Therefore, angle ADB = 90°.
- The angle BAC is subtended by the chord BC at point A. By the inscribed angle theorem, the angle BDC (subtended by the same chord BC at point D) will also be equal to angle BAC.
- Thus, angle BDC = angle BAC = 25°.
- In triangle ADB, we have:
- angle ADB = 90°
- angle BAC = 25°
- Let angle CAD = x (the angle we need to find).
- The sum of angles in triangle ADB is 180°.
- Therefore, we can write the equation:
angleADB+angleBAC+angleCAD=180°
- Substituting the known values:
90°+25°+x=180°
- Combine the known angles:
115°+x=180°
- Rearranging gives:
x=180°−115°=65°
- Therefore, angle CAD = 65°.
angle CAD=65°
Topper's Solved these Questions
Similar Questions
In a circle with centre O, AB is the diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=24∘ , then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB व्यास है तथा CD एक ऐसी जीवा है कि ABCD एक समलम्ब बन जाता है | यदि ∠BAC=24∘ है, तो ∠CAD का मान ज्ञात करें |
View SolutionIn a circle with centre O, AB is the diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=18∘, then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB व्यास है तथा एक ऐसी जीवा है कि ABCD एक समलम्ब बन जाता है | यदि ∠BAC=18∘ है, तो ∠CAD का मान ज्ञात करें |
View SolutionIn a circle with centre O, AB is a diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=28∘ ,then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB एक व्यास है तथा CD एक ऐसी जीवा है कि ABCD एक समलम्ब है | यदि ∠BAC=28∘ , है, तो कोण CAD ज्ञात करें |
View SolutionIn a circle with centre O, AB is the diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=40∘., then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB व्यास है और CD एक ऐसी जीवा है कि ABCD समलम्ब है | यदि ∠BAC=40∘ है, तो ∠CAD ज्ञात करें|
View SolutionIn a circle with centre O, AD is a diameter and AC is a chord. B is a point on AC, such that OB = 5 cm and ∠OBA=60∘. If ∠DOC=60∘, then what is the length of BC?
केंद्र O वाले एक वृत्त में, AD व्यास है तथा AC जीवा है | B, AC पर स्थित बिंदु है जो इस प्रकार है कि OB =5 सेमी तथा ∠OBA=60∘ है | यदि ∠DOC=60∘ है, तो BC की लंबाई ज्ञात करें |
View SolutionIn a circle with centre O, AD is a diameter and AC is a chord. Point B on AC such that OB = 7cm and ∠OBA=60∘. If ∠DOC=60∘, then what is the length of BC?
केंद्र वाले एक वृत्त में, AD एक व्यास है और AC एक जीवा है। AC पर एक बिंदु B इस प्रकार है की OB = 7 सेमी और ∠OBA=60∘ | यदि ∠DOC=60∘ है, तो BC की लंबाई क्या है?
View SolutionIn the given figure, BC is a chord and CD is a tangent through the point C. If ∠AOC=118∘, then find the ∠ACD.
दी गयी आकृति में, BC एक जीवा है तथा CD एक स्पर्श रेखा है जो C से जाती है। यदि ∠AOC=118∘ है, तो ∠ACD का मान ज्ञात कीजिए।
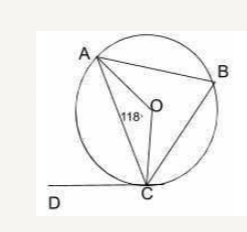
View SolutionThe tangent at a point A of a circle with centre O intersects the diameter PQ of the circle (when extended) at the point B. If ∠BAP=125∘, then ∠AQP is equal to:
केंद्र O के साथ एक वृत्त के बिंदु A पर स्पश्रेखा, बिंदु , B पर वृत्त के व्यास PQ ( जब विस्तारित) को काटती है यदि∠BAP=125∘ है, तो ∠AQP के ज्ञात करें ।
View SolutionAB is a diameter of a circle with centre O, and P is a point on the circle. If ∠POA=130∘, the ∠PBO is equal to:
AB केंद्र O के साथ एक वृत्त पर एक व्यास है, और P वृत्त का एक बिंदु है। यदि ∠POA=130∘, तो ∠PBO का मान ज्ञात करे|
View SolutionIn a circle with centre O, A diameter AB and a chord CD intersect each other at E, Ac and AD are joined. If ∠BOC=48∘ and ∠AOD=100∘, then what is the measure of ∠CEB ?
केंद्र O वाले एक वृत्त में, व्यास AB तथा जीवा CD एक दूसरे को E पर काटते हैं | AC तथा AD को मिलाया जाता है | यदि ∠BOC=48∘ है और ∠AOD=100∘ है, तो ∠CEB का मान ज्ञात करें |
View Solution