In a circle with centre O, AB is the diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=18∘, then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB व्यास है तथा एक ऐसी जीवा है कि ABCD एक समलम्ब बन जाता है | यदि
∠BAC=18∘ है, तो ∠CAD का मान ज्ञात करें |
72∘
36∘
54∘
18∘
To solve the problem, we need to find the angle CAD in the trapezium ABCD, where AB is the diameter of the circle and angle BAC is given as 18 degrees.
1. Draw the Circle and Label the Points:
- Draw a circle with center O.
- Mark the diameter AB.
- Draw a chord CD such that ABCD forms a trapezium.
2. Identify Given Angles:
- We know that angle BAC = 18 degrees.
3. Use the Property of Angles in a Circle:
- Since AB is the diameter, angle ACB (the angle subtended by the diameter at point C) is a right angle (90 degrees) according to the property of circles.
4. Calculate Angle ACB:
- In triangle ABC, we have:
- Angle BAC = 18 degrees
- Angle ACB = 90 degrees
- Therefore, we can find angle ABC using the sum of angles in a triangle:
Angle ABC=180−Angle BAC−Angle ACB=180−18−90=72 degrees
5. Use the Isosceles Triangle Property:
- Since OA = OB (both are radii of the circle), triangle OAB is isosceles.
- Therefore, angle OAB = angle OBA = 72 degrees (because angles opposite to equal sides are equal).
6. Find Angle CAD:
- In triangle OAC, we know:
- Angle OAC = angle OAB = 72 degrees.
- Angle AOC (the angle at the center) is twice the angle at the circumference, which is angle ABC:
Angle AOC=2×Angle ABC=2×72=144 degrees
- Now, in triangle OAC:
Angle CAD=180−Angle OAC−Angle AOC=180−72−144=36 degrees
Final Answer:
Thus, angle CAD = 36 degrees.
- Draw a circle with center O.
- Mark the diameter AB.
- Draw a chord CD such that ABCD forms a trapezium.
- We know that angle BAC = 18 degrees.
- Since AB is the diameter, angle ACB (the angle subtended by the diameter at point C) is a right angle (90 degrees) according to the property of circles.
- In triangle ABC, we have:
- Angle BAC = 18 degrees
- Angle ACB = 90 degrees
- Therefore, we can find angle ABC using the sum of angles in a triangle:
Angle ABC=180−Angle BAC−Angle ACB=180−18−90=72 degrees
- Since OA = OB (both are radii of the circle), triangle OAB is isosceles.
- Therefore, angle OAB = angle OBA = 72 degrees (because angles opposite to equal sides are equal).
- In triangle OAC, we know:
- Angle OAC = angle OAB = 72 degrees.
- Angle AOC (the angle at the center) is twice the angle at the circumference, which is angle ABC:
Angle AOC=2×Angle ABC=2×72=144 degrees
- Now, in triangle OAC:
Angle CAD=180−Angle OAC−Angle AOC=180−72−144=36 degrees
Thus, angle CAD = 36 degrees.
Topper's Solved these Questions
Similar Questions
In a circle with centre O, AB is the diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=25∘ , then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB व्यास है तथा CD एक ऐसी जीवा है कि ABCD एक समलम्ब बन जाता है | यदि ∠BAC=25∘ है, तो ∠CAD का मान ज्ञात करें |
View SolutionIn a circle with centre O, AB is the diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=24∘ , then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB व्यास है तथा CD एक ऐसी जीवा है कि ABCD एक समलम्ब बन जाता है | यदि ∠BAC=24∘ है, तो ∠CAD का मान ज्ञात करें |
View SolutionIn a circle with centre O, AB is the diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=40∘., then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB व्यास है और CD एक ऐसी जीवा है कि ABCD समलम्ब है | यदि ∠BAC=40∘ है, तो ∠CAD ज्ञात करें|
View SolutionIn a circle with centre O, AB is a diameter and CD is a chord such that ABCD is a trapezium. If ∠BAC=28∘ ,then ∠CAD is equal to:
केंद्र O वाले एक वृत्त में, AB एक व्यास है तथा CD एक ऐसी जीवा है कि ABCD एक समलम्ब है | यदि ∠BAC=28∘ , है, तो कोण CAD ज्ञात करें |
View SolutionIn the given figure, ABCD is a cyclic quadrilateral and AB is diameter. ∠ADC=140∘, then find ∠BAC :

View SolutionIn a circle with centre O, AD is a diameter and AC is a chord. B is a point on AC, such that OB = 5 cm and ∠OBA=60∘. If ∠DOC=60∘, then what is the length of BC?
केंद्र O वाले एक वृत्त में, AD व्यास है तथा AC जीवा है | B, AC पर स्थित बिंदु है जो इस प्रकार है कि OB =5 सेमी तथा ∠OBA=60∘ है | यदि ∠DOC=60∘ है, तो BC की लंबाई ज्ञात करें |
View SolutionIn a circle with centre O, AD is a diameter and AC is a chord. Point B on AC such that OB = 7cm and ∠OBA=60∘. If ∠DOC=60∘, then what is the length of BC?
केंद्र वाले एक वृत्त में, AD एक व्यास है और AC एक जीवा है। AC पर एक बिंदु B इस प्रकार है की OB = 7 सेमी और ∠OBA=60∘ | यदि ∠DOC=60∘ है, तो BC की लंबाई क्या है?
View SolutionIn the given figure, BC is a chord and CD is a tangent through the point C. If ∠AOC=118∘, then find the ∠ACD.
दी गयी आकृति में, BC एक जीवा है तथा CD एक स्पर्श रेखा है जो C से जाती है। यदि ∠AOC=118∘ है, तो ∠ACD का मान ज्ञात कीजिए।
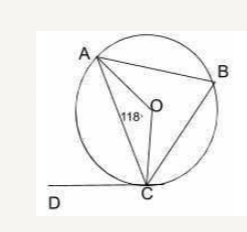
View SolutionIn a circle with centre O, A diameter AB and a chord CD intersect each other at E, Ac and AD are joined. If ∠BOC=48∘ and ∠AOD=100∘, then what is the measure of ∠CEB ?
केंद्र O वाले एक वृत्त में, व्यास AB तथा जीवा CD एक दूसरे को E पर काटते हैं | AC तथा AD को मिलाया जाता है | यदि ∠BOC=48∘ है और ∠AOD=100∘ है, तो ∠CEB का मान ज्ञात करें |
View SolutionAB is a diameter of a circle with centre O, and P is a point on the circle. If ∠POA=130∘, the ∠PBO is equal to:
AB केंद्र O के साथ एक वृत्त पर एक व्यास है, और P वृत्त का एक बिंदु है। यदि ∠POA=130∘, तो ∠PBO का मान ज्ञात करे|
View Solution
