The sides AB and AC of △ABC are produced to points D and E, respectively. The bisectors of ∠CBDand∠BCE meet at P. If ∠A=72∘, then the measure of ∠P is:
36∘
45∘
60∘
54∘
To solve for the measure of angle P in triangle ABC, where the sides AB and AC are extended to points D and E respectively, and the angle bisectors of angles CBD and BCE meet at point P, follow these steps:
1. Understand the Geometry:
- We have triangle ABC with angle A = 72°.
- The sides AB and AC are extended to points D and E respectively.
- We need to find the angle P formed by the intersection of the angle bisectors of angles CBD and BCE.
2. Identify Angles:
- Let angle A = 72°.
- The exterior angle at point B (angle CBD) can be expressed as:
Angle CBD=180°−Angle ABC
- The exterior angle at point C (angle BCE) can be expressed as:
Angle BCE=180°−Angle ACB
3. Use the Angle Bisector Theorem:
- The angle bisector of angle CBD will split it into two equal angles.
- Similarly, the angle bisector of angle BCE will also split it into two equal angles.
4. Calculate the Measure of Angle P:
- The angle P formed by the intersection of these two bisectors can be calculated using the formula:
Angle P=90°−12Angle A
- Substituting the value of angle A:
Angle P=90°−12×72°
- Calculate:
Angle P=90°−36°=54°
Final Answer:
The measure of angle P is 54°.
- We have triangle ABC with angle A = 72°.
- The sides AB and AC are extended to points D and E respectively.
- We need to find the angle P formed by the intersection of the angle bisectors of angles CBD and BCE.
- Let angle A = 72°.
- The exterior angle at point B (angle CBD) can be expressed as:
Angle CBD=180°−Angle ABC
- The exterior angle at point C (angle BCE) can be expressed as:
Angle BCE=180°−Angle ACB
- The angle bisector of angle CBD will split it into two equal angles.
- Similarly, the angle bisector of angle BCE will also split it into two equal angles.
- The angle P formed by the intersection of these two bisectors can be calculated using the formula:
Angle P=90°−12Angle A
- Substituting the value of angle A:
Angle P=90°−12×72°
- Calculate:
Angle P=90°−36°=54°
The measure of angle P is 54°.
Topper's Solved these Questions
Similar Questions
The sides AB and AC of △ABC are produced to points D and E, respectively. The bisectors of ∠CBD and ∠BCE meet at P. If ∠A=72∘, then the measure of ∠P is :
एक त्रिभुज ABC की भुजाएं AB और AC को क्रमशः बिंदु D तथा E तक बढ़ाया जाता है | ∠CBD तथा ∠BCE के समद्विभाजक P पर मिलते हैं | यदि ∠A=72∘ है, तो कोण P का मान ज्ञात करें
View SolutionThe sides AB and AC of △ABC are produced to P and Q respectively. The bisectors of ∠CBP and ∠BCQ meet at R. If the measure of ∠A is 44∘, then what is the measure of 12∠BRC?
त्रिभुज ABC की AB और AC भुजाएं क्रमशः P और Q बनाती हैं। ∠CBP और ∠BCQ के द्विभाजक R पर मिलते हैं। अगर ∠A का माप 44∘ है तो 12∠BRC का माप क्या है?
View Solution
Knowledge Check
The sides AB and AC of △ABC are produced to points D and E, respectiely. The bisectors of ∠CBD and ∠BCE meet at P. If ∠A=82∘, then the measure of ∠P is :
A54∘B60∘C36∘D49∘In figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of ∠PBCand∠QCB intersect at O. Then, ∠BOC is equal to
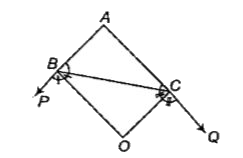 A90∘−12∠BACB12(∠PBC+∠QCB)C90∘+12∠BACDNone of the above
A90∘−12∠BACB12(∠PBC+∠QCB)C90∘+12∠BACDNone of the aboveIn △ABC ,∠B=68∘ and ∠C=32∘ . Sides AB and AC are produced to points D and E, respectively. The bisectors of ∠DBC and ∠BCE meet at F. What is the measure of ∠BFC ? /
△ABC में, ∠B=68∘ तथा ∠C=32∘ है | भुजाओं AB और AC को क्रमशः बिंदु D और E तक बढ़ाया जाता है | ∠DBC तथा ∠BCE के समद्विभाजक F पर मिलते हैं | कोण BFC का मान ज्ञात करें |A65∘B50∘C55∘D39∘
The sides AB and AC of △ABC are produced to P and Q respectively. The bisectors of ∠CBP and ∠BCQ meet at O. If the measure of ∠A is 44∘, then what is the measure of 12∠BOC?
एक त्रिभुज ABC की भुजाओं AB और AC को क्रमशः P और Q तक बढ़ाया जाता है | ∠CBP और ∠BCQ के समद्विभाजक O पर मिलते हैं| यदि कोण A का मान 44∘ है, तो 12∠BOC का मान क्या होगा ?
View SolutionIn △ABC ,∠B=68∘ and ∠C=32∘ . Sides AB and AC are produced to points D and E, respectively. The bisectors of ∠DBC and ∠BCE meet at F. What is the measure of ∠BFC ? /
△ABC में, ∠B=68∘ तथा ∠C=32∘ है | भुजाओं AB और AC को क्रमशः बिंदु D और E तक बढ़ाया जाता है | ∠DBC तथा ∠BCE के समद्विभाजक F पर मिलते हैं | कोण BFC का मान ज्ञात करें |
View SolutionIn a △ABC, the sides AB and AC are extended to P and Q respectively. The bisectors of ∠PBC and ∠QCB intersect at a point R. If ∠R=66∘, then the measure of ∠A is :
त्रिभुज ABC में, AB और AC भुजाओं को क्रमशः P और Q तक बढ़ाया जाता है| ∠PBC तथा ∠QCB के द्विभाजक एक बिंदु R पर मिलते हैं | यदि ∠R=66∘, है, तो कोण A का मान ज्ञात करें |
View SolutionThe sides AB and AC of a △ABC are extended to P and Q respectively. If the bisectors of ∠PBC and ∠QCB intersect at O, and ∠A=92∘, then ∠BOC is equal to:
एक त्रिभुज ABC की भुजाओं AB और AC को क्रमशः P तथा Q तक बढ़ाया जाता है | यदि ∠PBC तथा ∠QCB के समद्विभाजक एक दूसरे को O पर काटते हैं तथा ∠A=92∘ है, तो ∠BOC किसके बराबर है ?
View SolutionIn △ABC ,∠A=72∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=72∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के समद्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान ज्ञात करें |
View Solution
