Question

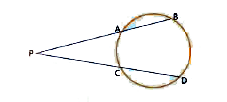
Chords AB and CD of a circle intersect externally at P. If AB = 6 cm, CD = 3 cm and PB = 4 cm, then the length (in cm) of PD is :
एक वृत्त की जीवायें AB और CD एक दूसरे को बाहर से P पर काटती हैं | यदि AB = 6 सेमी,CD =3 सेमी और PB =4 सेमी है, तो PD की लंबाई (सेमी में ) ज्ञात करें |

Options

A. 5
B. 6
C. 2
D. 7

Explanation

To find the length of PD, we can use the property of intersecting chords in a circle. The property states that if two chords AB and CD intersect at an external point P, then the following relationship holds:

$$PB\times PA=PD\times PC$$

Where:
- $$PB$$ is the length from point P to point B,
- $$PA$$ is the length from point P to point A,
- $$PD$$ is the length from point P to point D,
- $$PC$$ is the length from point P to point C.

Step 1: Identify the lengths given in the problem.
- \( AB = 6 \, \text{cm} \)
- \( CD = 3 \, \text{cm} \)
- \( PB = 4 \, \text{cm} \)

From the length of chord AB, we can find \( PA \):
\( PA = AB - PB = 6 \, \text{cm} - 4 \, \text{cm} = 2 \, \text{cm} \)

Step 2: Calculate \( PA \) and \( PC \).
Since \( CD = 3 \, \text{cm} \), we can express \( PC \) in terms of \( PD \):
\( PC = CD + PD = 3 \, \text{cm} + PD \)

Step 3: Substitute the values into the intersecting chords formula.
Now we can substitute \( PB \), \( PA \), and \( PC \) into the equation:
\( PB \times PA = PD \times PC \)
\( 4 \times 10 = PD \times (3 + PD) \)

Step 4: Simplify the equation.
Calculating the left side:
\( 4 \times 10 = 40 \)
So, we have:
\( 40 = PD \times (3 + PD) \)

Step 5: Rearrange the equation.
This leads us to:
\( PD^2 + 3PD - 40 = 0 \)

Step 6: Factor the quadratic equation.
Now we can factor the quadratic equation:
\( (PD + 8)(PD - 5) = 0 \)

Step 7: Solve for \( PD \).
Setting each factor to zero gives us:
1. \( PD + 8 = 0 \) → \( PD = -8 \) (not valid since length cannot be negative)
2. \( PD - 5 = 0 \) → \( PD = 5 \)

Thus, the length of \( PD \) is:
\( PD = 5 \, \text{cm} \)

Final Answer:
The length of PD is 5 cm.

---