Chords AB and CD of a circle intersect at a point P inside the circle. If AB = 10 cm. AP = 4 cm and PC = 5 cm, then CD is equal to:
एक वृत्त की जीवायें AB और CD वृत्त के भीतर स्थित बिंदु P पर एक दूसरे को काटती हैं | यदि AB =10 सेमी,AP = 4 सेमी और PC = 5 सेमी है, तो CD का मान क्या होगा ?
4.8 cm
6.8 cm
9.8 cm
7.8 cm
To find the length of chord CD in the given circle, we can use the intersecting chords theorem, which states that if two chords intersect each other inside a circle, then the products of the lengths of the segments of each chord are equal.
Let's denote the lengths as follows:
- Let AB=10cm
- Let AP=4cm
- Let PB=AB−AP=10−4=6cm
- Let PC=5cm
- Let PD be the unknown length we need to find.
According to the intersecting chords theorem:
AP×PB=CP×PD
Substituting the known values:
4×6=5×PD
Calculating the left side:
24=5×PD
Now, we can solve for PD:
PD=245=4.8cm
Now that we have PD, we can find the total length of chord CD:
CD=CP+PD=5+4.8=9.8cm
Thus, the length of chord CD is 9.8cm.
- Let AB=10cm
- Let AP=4cm
- Let PB=AB−AP=10−4=6cm
- Let PC=5cm
- Let PD be the unknown length we need to find.
AP×PB=CP×PD
4×6=5×PD
24=5×PD
PD=245=4.8cm
CD=CP+PD=5+4.8=9.8cm
Topper's Solved these Questions
Similar Questions
Two chords AB and CD of a circle intersect at a point P inside the circle. If AB = 7cm , PC = 2 cm and AP = 4 cm, then CD is equal to:
एक वृत्त की दो जीवाएं AB और CD वृत्त के भीतर बिंदु P पर एक दूसरे को काटती हैं | यदि AB = 7 सेमी, PC = 2 सेमी और AP = 4 सेमी है, तो CD किसके बराबर होगा ?
View SolutionChords AB and CD of a circle , when produced, meet at point P outside the circle. If AB = 6 cm, CD = 3 cm and PD = 5 cm, then PB is equal to :
एक वृत्त की जीवाएं AB और CD को जब बढ़ाया जाता है तो वे वृत्त के बाहर बिंदु P पर मिलती हैं | यदि AB = 6 सेमी, CD = 3 सेमी और PD = 5 सेमी है, तो PB का मान क्या होगा ?
View Solution
Knowledge Check
Chords AB and CD of a circle intersect externally at P. If AB=6cm,CD=3cmandPD=5cm, then the length of PB is
A5 cmB7.35 cmC6 cmD4 cmTwo chords AB and CD of a circle intersect each other at P internally. If AP = 3.5 cm, PC = 5 cm, and DP = 7 cm, then what is the measure of PB?
A8 cmB12 cmC10 cmD10.5 cmTwo chords AB and CD of a circle are produced to intersect each other at point P outside the circle. If AB=7 cm, BP = 4.2 cm and PD = 2.8 cm, then the length of CD is: /
एक वृत्त की दो जीवाओं AB और CD को बढ़ाया जाता है जो एक-दूसरे को वृत्त के बाहर बिंदु ? पर काटती हैं| यदि AB = 7 सेमी, BP = 4.2 सेमी तथा तथा PD = 2.8 सेमी है, तो CD की लंबाई कितनी है ?A15.8 cmB12 cmC14 cmD14.6 cm
Two chords AB and CD of a circle, when produced, meet at a point P outside the circle. If AB = 6 cm , PB = 5 cm , PD = 4 cm, then CD is equal to :
एक वृत्त की दो जीवाओं AB और CD को जब बढ़ाया जाता है तो वे वृत्त के बाहर बिंदु P पर मिलती हैं | यदि AB=6 सेमी, PB = 5 सेमी और PD = 4 सेमी है, तो CD का मान किसके बराबर है ?
View SolutionChords AB and CD of a circle intersect externally at P. If AB = 6 cm, CD = 3 cm and PB = 4 cm, then the length (in cm) of PD is :
एक वृत्त की जीवायें AB और CD एक दूसरे को बाहर से P पर काटती हैं | यदि AB = 6 सेमी,CD =3 सेमी और PB =4 सेमी है, तो PD की लंबाई (सेमी में ) ज्ञात करें |
View SolutionTwo chords AB and CD of a circle are produced to intersect each other at point P outside the circle. If AB=7 cm, BP = 4.2 cm and PD = 2.8 cm, then the length of CD is: /
एक वृत्त की दो जीवाओं AB और CD को बढ़ाया जाता है जो एक-दूसरे को वृत्त के बाहर बिंदु ? पर काटती हैं| यदि AB = 7 सेमी, BP = 4.2 सेमी तथा तथा PD = 2.8 सेमी है, तो CD की लंबाई कितनी है ?
View SolutionTwo chords, AB and CD of circle meet at a point O, outside the circle. It is given that AB = 7 cm, CD = 4 cm, OB = 5 cm. What is the length of OD?
एक वृत्त की दो जीवाएं AB और CD किसी बिंदु O पर मिलती हैं जो वृत्त के बाहर है | यह दिया गया है कि AB = 7 सेमी, CD = 4 सेमी, OB = 5 सेमी है | OD की लंबाई क्या है ?
View SolutionIn the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point P within the circle. If AB = 15 cm, PB = 9 cm, CP = 3 cm, then find the length of PD.
दी गयी आकृति में, Oवृत्त का केंद्र है। इसकी दो जीवाएँ AB और CD एक-दूसरे को वृत्त के भीतर बिंदु P पर प्रतिच्छेद करती हैं। यदि AB =15 सेमी, PB = 9 सेमी, CP = 3 सेमी है, तो PD की लंबाई ज्ञात कीजिए।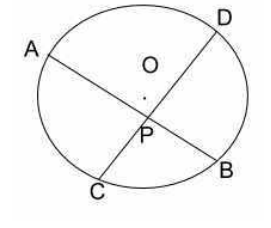
View Solution
