In a circle, AB is the diameter and CD is a chord. AB and CD produced meet at a point P, outside the circle. If PD = 15.3 cm, CD = 11.9 cm and AP = 30.6 cm, then the radius of the circle is:
एक वृत्त में, AB व्यास है तथा CD एक जीवा है | AB तथा CD को बढ़ाया जाता है जो वृत्त से बाहर एक बिंदु P पर मिलती हैं | यदि PD = 15.3 सेमी, CD = 11.9 सेमी तथा AP = 30.6 सेमी है, तो वृत्त की त्रिज्या कितनी है ?
8 cm
8.5 cm
9 cm
7.5 cm
To find the radius of the circle given the parameters of the problem, we can use the Power of a Point theorem. According to this theorem, for a point P outside a circle, the product of the lengths of the segments from the point to the points of intersection with the circle is constant.
1. Identify the given lengths:
- PD=15.3cm
- CD=11.9cm
- AP=30.6cm
2. Calculate the length of PC:
Since CD is a chord, we can express PC as:
PC=PD+CD=15.3cm+11.9cm=27.2cm
3. Use the Power of a Point theorem:
According to the theorem:
PA×PB=PC×PD
Here, PA=AP=30.6cm and PB=PA−AB. Since AB is the diameter, we can express PB as:
PB=PA−AB
We need to find AB first.
4. Calculate AB:
The diameter AB can be expressed as:
AB=AP−PD=30.6cm−15.3cm=15.3cm
5. Calculate PB:
Now substituting the value of AB:
PB=30.6cm−15.3cm=15.3cm
6. Substitute values into the Power of a Point equation:
PA×PB=PC×PD
30.6cm×15.3cm=27.2cm×15.3cm
7. Calculate the left side:
30.6×15.3=468.18cm2
8. Calculate the right side:
27.2×15.3=416.16cm2
9. Since both sides are equal, we can find the radius:
The diameter AB is 15.3cm, thus the radius r is:
r=AB2=15.32=7.65cm
Final Answer:
The radius of the circle is 7.65cm.
- PD=15.3cm
- CD=11.9cm
- AP=30.6cm
Since CD is a chord, we can express PC as:
PC=PD+CD=15.3cm+11.9cm=27.2cm
According to the theorem:
PA×PB=PC×PD
Here, PA=AP=30.6cm and PB=PA−AB. Since AB is the diameter, we can express PB as:
PB=PA−AB
We need to find AB first.
The diameter AB can be expressed as:
AB=AP−PD=30.6cm−15.3cm=15.3cm
Now substituting the value of AB:
PB=30.6cm−15.3cm=15.3cm
PA×PB=PC×PD
30.6cm×15.3cm=27.2cm×15.3cm
30.6×15.3=468.18cm2
27.2×15.3=416.16cm2
The diameter AB is 15.3cm, thus the radius r is:
r=AB2=15.32=7.65cm
The radius of the circle is 7.65cm.
Topper's Solved these Questions
Similar Questions
Chords AB and CD of a circle , when produced, meet at point P outside the circle. If AB = 6 cm, CD = 3 cm and PD = 5 cm, then PB is equal to :
एक वृत्त की जीवाएं AB और CD को जब बढ़ाया जाता है तो वे वृत्त के बाहर बिंदु P पर मिलती हैं | यदि AB = 6 सेमी, CD = 3 सेमी और PD = 5 सेमी है, तो PB का मान क्या होगा ?
View SolutionTwo chords AB and CD of a circle are produced to intersect each other at point P outside the circle. If AB=7 cm, BP = 4.2 cm and PD = 2.8 cm, then the length of CD is: /
एक वृत्त की दो जीवाओं AB और CD को बढ़ाया जाता है जो एक-दूसरे को वृत्त के बाहर बिंदु ? पर काटती हैं| यदि AB = 7 सेमी, BP = 4.2 सेमी तथा तथा PD = 2.8 सेमी है, तो CD की लंबाई कितनी है ?
View Solution
Knowledge Check
Chords AB and CD of a circle intersect at a point P inside the circle. If AB = 10 cm, AP = 4 cm and PC = 5 cm, then CD is equal to:
A4.8 cmB6.8 cmC9.8 cmD7.8 cmTwo chords AB and CD of a circle are produced to intersect each other at point P outside the circle. If AB=7 cm, BP = 4.2 cm and PD = 2.8 cm, then the length of CD is: /
एक वृत्त की दो जीवाओं AB और CD को बढ़ाया जाता है जो एक-दूसरे को वृत्त के बाहर बिंदु ? पर काटती हैं| यदि AB = 7 सेमी, BP = 4.2 सेमी तथा तथा PD = 2.8 सेमी है, तो CD की लंबाई कितनी है ?A15.8 cmB12 cmC14 cmD14.6 cmVinod have 20 rupees. He bought 1, 2, 5 rupee stamps. They are different in numbers by the reason of no change, the shop keeper gives 3 one rupee stamps. So how many stamps Vinod have ?
AA) 10BB) 18CC) 12DD) 15
Two chords AB and CD of a circle, when produced, meet at a point P outside the circle. If AB = 6 cm , PB = 5 cm , PD = 4 cm, then CD is equal to :
एक वृत्त की दो जीवाओं AB और CD को जब बढ़ाया जाता है तो वे वृत्त के बाहर बिंदु P पर मिलती हैं | यदि AB=6 सेमी, PB = 5 सेमी और PD = 4 सेमी है, तो CD का मान किसके बराबर है ?
View SolutionIn a circle, AB and DC are two chords. When AB and DC are produced, they meet at P. If PC = 5.6 cm, PB = 6.3 cm and AB = 7.7 cm, the the length of CD is :
/ एक वृत्त में, AB तथा DC दो जीवाएं है | जब AB और DC को बढ़ाया जाता है, तो वे P पर मिलती हैं | यदि PC = 5.6 सेमी , PB = 6.3 सेमी और AB = 7.7 सेमी है, तो CD की लंबाई ज्ञात करें |
View SolutionIn a circle, AB and DC are two chords. When AB and DC are produced, they meet at P. If PC = 5.6 cm, PB = 6.3 cm and AB = 7.7 cm, then the length of CD is:
View SolutionAB and CD are parallel chords of a circle 3 cm apart. If AB = 4 cm, CD = 10 cm, then what is the radius of the circle ?
View SolutionIn the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point P within the circle. If AB = 15 cm, PB = 9 cm, CP = 3 cm, then find the length of PD.
दी गयी आकृति में, Oवृत्त का केंद्र है। इसकी दो जीवाएँ AB और CD एक-दूसरे को वृत्त के भीतर बिंदु P पर प्रतिच्छेद करती हैं। यदि AB =15 सेमी, PB = 9 सेमी, CP = 3 सेमी है, तो PD की लंबाई ज्ञात कीजिए।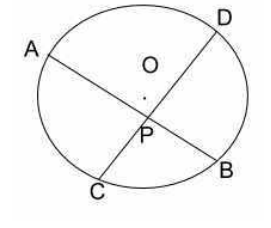
View Solution
