In a circle, AB and DC are two chords. When AB and DC are produced, they meet at P. If PC = 5.6 cm, PB = 6.3 cm and AB = 7.7 cm, then the length of CD is:
8.35 cm
9 cm
10.15 cm
9.25 cm
To find the length of CD in the given circle with chords AB and DC, we can use the theorem of external division of chords. Here’s a step-by-step solution:
Step 1: Understand the Given Information
We have:
- Length of chord AB = 7.7 cm
- PB (the segment from point P to point B) = 6.3 cm
- PC (the segment from point P to point C) = 5.6 cm
Step 2: Calculate PA
PA is the total length from point P to point A, which can be calculated as:
PA=PB+AB
Substituting the values:
PA=6.3cm+7.7cm=14cm
Step 3: Express PD in Terms of CD
PD is the total length from point P to point D. Since PD includes segment PC and the unknown length CD, we can express it as:
PD=PC+CD
Substituting the value of PC:
PD=5.6cm+CD
Step 4: Apply the Theorem of External Division
According to the theorem of external division, we have:
PB×PA=PC×PD
Substituting the known values:
6.3×14=5.6×(5.6+CD)
Step 5: Calculate the Left Side
Calculating the left side:
6.3×14=88.2
Step 6: Set Up the Equation
Now we have:
88.2=5.6×(5.6+CD)
Step 7: Distribute on the Right Side
Distributing the right side:
88.2=5.6×5.6+5.6×CD
Calculating 5.6×5.6:
5.6×5.6=31.36
So the equation becomes:
88.2=31.36+5.6×CD
Step 8: Isolate the CD Term
Now, isolate 5.6×CD:
5.6×CD=88.2−31.36
Calculating the right side:
88.2−31.36=56.84
So we have:
5.6×CD=56.84
Step 9: Solve for CD
Now, divide both sides by 5.6 to find CD:
CD=56.845.6
Calculating this gives:
CD=10.15cm
Final Answer
The length of CD is 10.15cm.
---
We have:
- Length of chord AB = 7.7 cm
- PB (the segment from point P to point B) = 6.3 cm
- PC (the segment from point P to point C) = 5.6 cm
PA is the total length from point P to point A, which can be calculated as:
PA=PB+AB
Substituting the values:
PA=6.3cm+7.7cm=14cm
PD is the total length from point P to point D. Since PD includes segment PC and the unknown length CD, we can express it as:
PD=PC+CD
Substituting the value of PC:
PD=5.6cm+CD
According to the theorem of external division, we have:
PB×PA=PC×PD
Substituting the known values:
6.3×14=5.6×(5.6+CD)
Calculating the left side:
6.3×14=88.2
Now we have:
88.2=5.6×(5.6+CD)
Distributing the right side:
88.2=5.6×5.6+5.6×CD
Calculating 5.6×5.6:
5.6×5.6=31.36
So the equation becomes:
88.2=31.36+5.6×CD
Now, isolate 5.6×CD:
5.6×CD=88.2−31.36
Calculating the right side:
88.2−31.36=56.84
So we have:
5.6×CD=56.84
Now, divide both sides by 5.6 to find CD:
CD=56.845.6
Calculating this gives:
CD=10.15cm
The length of CD is 10.15cm.
Topper's Solved these Questions
Similar Questions
In a circle, AB and DC are two chords. When AB and DC are produced, they meet at P. If PC = 5.6 cm, PB = 6.3 cm and AB = 7.7 cm, the the length of CD is :
/ एक वृत्त में, AB तथा DC दो जीवाएं है | जब AB और DC को बढ़ाया जाता है, तो वे P पर मिलती हैं | यदि PC = 5.6 सेमी , PB = 6.3 सेमी और AB = 7.7 सेमी है, तो CD की लंबाई ज्ञात करें |
View SolutionABCD is a cyclic quadrilateral. AB and CD when produced meet at P, if PA = 8 cm, PB = 6 cm, PC = 4 cm, then the length (in cm) of PD is.
View Solution
Knowledge Check
Chords AB and CD of a circle intersect externally at P. If AB=6cm,CD=3cmandPD=5cm, then the length of PB is
A5 cmB7.35 cmC6 cmD4 cmTwo chords AB and CD of a circle are produced to intersect each other at point P outside the circle. If AB=7 cm, BP = 4.2 cm and PD = 2.8 cm, then the length of CD is: /
एक वृत्त की दो जीवाओं AB और CD को बढ़ाया जाता है जो एक-दूसरे को वृत्त के बाहर बिंदु ? पर काटती हैं| यदि AB = 7 सेमी, BP = 4.2 सेमी तथा तथा PD = 2.8 सेमी है, तो CD की लंबाई कितनी है ?A15.8 cmB12 cmC14 cmD14.6 cmQuadrilateral ABCD circumscribes a circle. If AB = 8 cm, BC = 7 cm and CD = 6 cm, then the length of AD is:
A7 cmB6.8 cmC7.5 cmD6 cm
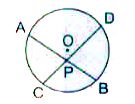
In the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point P within the circle. If AB = 18 cm, PB = 8 cm, CP = 5 cm, then find the length of CD.
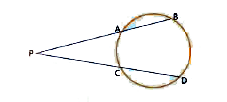
View SolutionIn the given figure,chords AB and CD of a circle intersect externally at P. AB=4 cm,CD=11 cm and PD=15 cm,then the length of PB is:
View SolutionThe two chords AB and CD of a circle intersect at point P, such that BP=4 cm, PD=5 cm, and CP=8 cm. find the length of chord AB.
View Solution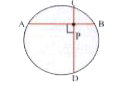
In the above circle two chords AB and CD intersect at 90∘. If AP = 8 cm, PB = 4 cm, PC = 3 cm and PD = 9 cm, then radius of circle is
View SolutionIf AB and CD are two chords of a circle intersected at point O. If CO = 4cm and OD = 3.5 cm and AB = 9 cm then find the length of smaller between AO and BO.
View Solution